

Next: D..3.1 Mathematicaでやってみる
Up: D. Mathematicaの多変数の微積分への応用
Previous: D..2.1 Mathematicaでやってみる
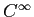 級の
級の
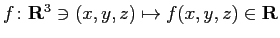 と、
と、
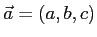 ,
,
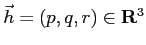 に対して
に対して
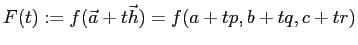
(
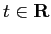
)
とおくとき、以下の問に答えよ。
- (1)
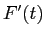 ,
, 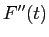 を計算せよ (
を計算せよ (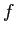 を使って表せ)。
を使って表せ)。
- (2)
- 自然数
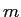 に対して
に対して
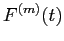 を
を 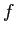 を用いて表す式を推定し、
帰納法を用いて証明せよ。
を用いて表す式を推定し、
帰納法を用いて証明せよ。
Subsections


Next: D..3.1 Mathematicaでやってみる
Up: D. Mathematicaの多変数の微積分への応用
Previous: D..2.1 Mathematicaでやってみる
桂田 祐史
2013-04-09