最初に二つの言葉を定義する。
行列
![]() が下三角行列 (lower triangluar
matrix) であるとは、対角線の上にある成分がすべて 0
である、つまり
が下三角行列 (lower triangluar
matrix) であるとは、対角線の上にある成分がすべて 0
である、つまり
が成り立つことと定義する。
同様に、
![]() が上三角行列 (upper triangular
matrix) であるとは、
対角線の下にある成分がすべて 0
である、つまり
が上三角行列 (upper triangular
matrix) であるとは、
対角線の下にある成分がすべて 0
である、つまり
が成り立つことと定義する。
目で見えるように書くと
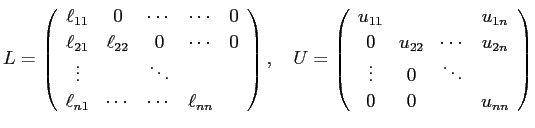
ということである。
| LU 分解 |
|
行列
を満たす下三角行列 |
Gauss の消去法の前進消去段階では、
係数行列に行に関する基本変形を施して上三角行列 (それを ![]() とおく) に
変形したが、
行に関する基本変形は、基本行列を左からかけることで表現できる。
Gauss の消去法では、これら基本行列はすべて正則な下三角行列である。
そこで、この変形は
とおく) に
変形したが、
行に関する基本変形は、基本行列を左からかけることで表現できる。
Gauss の消去法では、これら基本行列はすべて正則な下三角行列である。
そこで、この変形は
とかける。これから
となるが、
![\begin{jlemma}\upshape
\begin{enumerate}[(1)]
\item
下三角行列全体は�...
...��行列全体
は乗法について群をなす)。
\end{enumerate}\end{jlemma}](img103.png)
|
さて、それでは Gauss の消去法はいつでも出来るかというと、 (掃き出し法との類推ですぐ分かるように) 対角成分に 0 が現われたらダメになるわけである。 この場合は、行を適当に交換することで消去が出来るようになる。

|
正則行列 ![]() の LU 分解はたとえ存在しても一意ではないが、
の LU 分解はたとえ存在しても一意ではないが、
![]() を
を
の形に分解する LDU 分解は一意である。