例えば
- 有限回の四則では exact (厳密) に解けない問題がほとんど。
- 「反復法」で多くの問題が解ける。
すなわち、真の解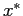 をある列
をある列 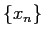 の極限としてとらえ
(
の極限としてとらえ
(
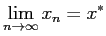 )、 十分大きな
)、 十分大きな 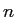 に対して
に対して 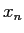 を
を
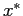 の近似として採用する。近似解ではあるが、
コンピューターで数値計算する限り、
有限精度であることは避けられないので、
exact な方法 (もしそれがあったとして) とほとんど差がない5。
の近似として採用する。近似解ではあるが、
コンピューターで数値計算する限り、
有限精度であることは避けられないので、
exact な方法 (もしそれがあったとして) とほとんど差がない5。
コンピューターで方程式を扱う場合、 コンピューターならではのやり方があります。 有限回の計算で真の解 (無限精度の解, 「厳密解」 (exact solution) とも呼ばれる) を求めることはあきらめて、 真の解を求めるには無限回の演算が必要になるけれど、 有限の要求精度を持つ近似解は、そこそこの回数の基本的な演算 (四則演算) で求まるような方法を採用する、 というものです。 従って、アルゴリズムは大抵の場合、 繰り返しのあるもの -- 反復法 -- になります。

厳密解の「厳密」は、論理的に厳密というのとは関係がなくて、 論理的に厳密であることと、近似解であることは相反するものではない、 という言い方も出来るでしょう。