古代ギリシャの時代から、
円周率は無理数ではないかと想像されていたと思いますが、
実際に「円周率は無理数である」ことを証明したのは、
ハインリッヒ・ランベルト (Johann Heinrich Lambert,
1728-1777, Mülhausen (Mulhouse, 現在のフランス) に生まれ、
Berlin にて没する,
物理・数学・地図投影法に業績がある) です (1761 年)。
彼は ![]() の連分数展開
の連分数展開
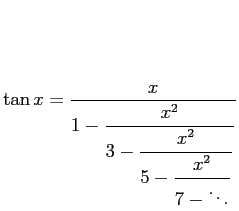
を用いて、 「
代数学を学ぶと、 超越数 (transcendental number) という概念を学びます。 「円周率は超越数」です (要するに整数係数の多項式の根にはならない)。 これを証明したのは、 リンデマン (Carl Louis Ferdinand von Lindemann, 1852-1939, 巨人 Hilbert の師匠としても有名5) という人でした (1822年)。