

Next: 5.1 �$BFsJ,K!�(B (bisection method)
Up: 5 �$BHs@~7AJ}Dx<0$r7W;;5!$G2r$/�(B
Previous: 5 �$BHs@~7AJ}Dx<0$r7W;;5!$G2r$/�(B
�$B$^$:�(B
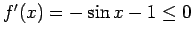 (
(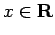 ) �$B$G!"FC$K�(B
) �$B$G!"FC$K�(B
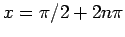 (
(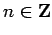 ) �$B0J30$N$H$3$m$G$O�(B
) �$B0J30$N$H$3$m$G$O�(B 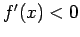 �$B$G$"$k$+$i!"�(B
�$B$G$"$k$+$i!"�(B
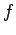 �$B$O695A$NC1D48:>/4X?t$G$"$k!#�(B
�$B$=$7$F�(B
�$B$O695A$NC1D48:>/4X?t$G$"$k!#�(B
�$B$=$7$F�(B 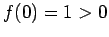 ,
,
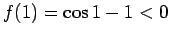 �$B$f$(!"�(B
�$BCf4VCM$NDjM}$K$h$C$F!"�(B
�$BJ}Dx<0�(B
�$B$f$(!"�(B
�$BCf4VCM$NDjM}$K$h$C$F!"�(B
�$BJ}Dx<0�(B 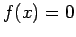 �$B$O6h4V�(B
�$B$O6h4V�(B 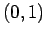 �$BFb$K>/$J$/$H$b0l$D$N2r$r;}$D$,!"�(B
�$BFb$K>/$J$/$H$b0l$D$N2r$r;}$D$,!"�(B
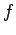 �$B$NC1D4@-$+$i$=$l$O�(B
�$B$NC1D4@-$+$i$=$l$O�(B 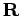 �$BA4BN$G$?$@0l$D$N2r$G$"$k$3$H$,J,$+$k!#�(B
�$BA4BN$G$?$@0l$D$N2r$G$"$k$3$H$,J,$+$k!#�(B


Next: 5.1 �$BFsJ,K!�(B (bisection method)
Up: 5 �$BHs@~7AJ}Dx<0$r7W;;5!$G2r$/�(B
Previous: 5 �$BHs@~7AJ}Dx<0$r7W;;5!$G2r$/�(B
Masashi Katsurada
�$BJ?@.�(B20�$BG/�(B10�$B7n�(B18�$BF|�(B