3 色々試す

この節で、「kvのドキュメント」と行っているのは、 「kv-intro.pdf」 のことを指す。

次は2次方程式のプログラムである。

quadratic_eq_kv.cpp

/*
 * quadratic_eq_kv.cpp
 *  g++ -I/usr/local/include -o quadratic_eq_kv quadratic_eq_kv.cpp
 */

#include <iostream>
#include <iomanip>
#include <cmath>
#include <kv/interval.hpp>
#include <kv/rdouble.hpp>
using namespace std;

int main(void)
{
  double _a,_b,_c;
  kv::interval<double> a,b,c,D;
  cout << setprecision(15);
  cout.setf(ios::fixed, ios::floatfield);
  cout << "a,b,c: ";
  cin >> _a >> _b >> _c;
  a = _a; b = _b; c = _c;
  D = b * b - 4 * a * c;
  if (D >= 0)
    cout << setw(20) << (-b+sqrt(D))/(2*a) << ", " << endl
         << setw(20) << (-b-sqrt(D))/(2*a) << endl;
  else
    cout << setw(20) << -b/(2*a) << "±"
         << setw(20) << sqrt(-D)/(2*a) << " i" << endl;
  return 0;
}

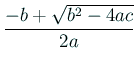これで「kvのドキュメント」p. 16に書いてあることを追試してみる。 $\vert 4ac\vert\ll b^2$ であるとき、 $\sqrt{b^2-4ac}\kinji\vert b\vert$ となるので、桁落ちが起こるという有名な話。 $b>0$ のときは $-b+\sqrt{b^2-4ac}$ の計算で、 $b<0$ のときは $-b-\sqrt{b^2-4ac}$ の計算で桁落ちが発生する。 $a=1$, $b=10^{15}$, $c=10^{14}$ とすると、 $\dfrac{-b+\sqrt{b^2-4ac}}{2a}$ の精度が低くなるはず。

kvのドキュメントの 16 ページ

% ./quadratic_eq_kv
a,b,c: 1 1e15 1e14
                   [-0.1875,-0.0625],
                   [-1000000000000000,-999999999999999.75]

最初の区間 [-0.1875,-0.0625] の幅が妙に大きくなってしまっている。 区間演算でないときは、精度が落ちていることに気付きにくいが、 はっきり分かる (Mathematica を使って多倍長計算した結果と比べるとか、 分子の有理化をした結果と比べるとか、そういうのをサボっても、 何かマズいことが起こっていることが分かる) のは区間演算を使う利点である。

次は、 interval<double> と interval<kv::dd> を使い比べる、 という話である (double は(2)倍精度だけれど、 kv::dd は4倍精度で、高精度計算出来る、という話)。

kvのドキュメント 33ページのソースプログラム

//
// http://verifiedby.me/kv/kv-intro.pdf
// 33ページ
// g++ -I/usr/local/include -I/opt/local/include p33.cpp

#include <kv/interval.hpp> // 区間演算
#include <kv/rdouble.hpp> // double の方向付き丸めを定義

int main()
{
  kv::interval<double>s, x;
  std :: cout.precision(17) ;

  s=0;
  for (int i=1; i<=1000; i++) {
    x=i;
    s += 1/x;
  }
  std::cout << s << "\n";
}

g++ -O3 -I/usr/local/include -I/opt/local/include -o p33 p33.cpp

kvのドキュメント 33ページの実行例

% ./p33
[7.485470860549956,7.4854708605508238]

kvのドキュメント 35ページのソースプログラム (dd型の利用)

//
// http://verifiedby.me/kv/kv-intro.pdf
// 35ページ
// g++ -I/usr/local/include -I/opt/local/include p35.cpp

#include <kv/interval.hpp> // 区間演算
#include <kv/dd.hpp> // double-double
#include <kv/rdd.hpp> // dd の方向付き丸めを定義

int main()
{
  kv::interval<kv::dd>s, x;
  std :: cout.precision(34) ;

  s=0;
  for (int i=1; i<=1000; i++) {
    x=i;
    s += 1/x;
  }
  std::cout << s << "\n";
}

kvのドキュメント 35ページの実行例

% ./p35
[7.485470860550344912656518204308257,7.485470860550344912656518204360964]

Profilならば 7.4854708605503449126565182043[08257,60964]と表示してくれるのに。