

Next: この文書について...
Up: 平面曲線
Previous: 6.11 アステロイド
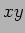 平面上で、
方程式
平面上で、
方程式
|
(☆) |
![$\displaystyle \left[(x-1)^2+y^2\right] \left[(x+1)^2+y^2\right]=a^4$](img132.png)  |
で定められる曲線を
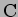 とするとき、以下の問に答えよ。
とするとき、以下の問に答えよ。
- (1)
- 式 (☆) を
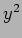 について解いて、
について解いて、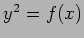 の形に表わせ。
の形に表わせ。
- (2)
-
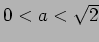 であるとき、関数
であるとき、関数 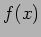 の増減を調べよ。
の増減を調べよ。
- (3)
-
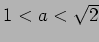 であるときの曲線
であるときの曲線
 の概形を描け。
の概形を描け。
(二定点からの距離の積が一定である曲線で、
Cassini の橙形と呼ばれているもの。)
- (1)
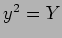 とおくと、(☆) は
とおくと、(☆) は
となる。整理して、
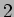 次方程式の解の公式から
次方程式の解の公式から
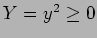 でなければならないので、複号のうち
でなければならないので、複号のうち  は捨てて
は捨てて
- (2)
-
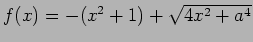 とおくと、
とおくと、
ゆえに 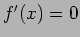 となるのは、
となるのは、
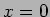 または
または
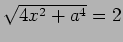 のときである。
のときである。
仮定
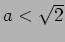 より
より 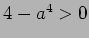 であるので、
であるので、
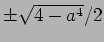 は相異なる実数であることに注意する。
これから関数
は相異なる実数であることに注意する。
これから関数 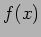 の増減表は
の増減表は
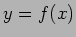 のグラフと
のグラフと 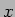 軸との交点を
調べる。
軸との交点を
調べる。
これから
- (i)
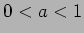 のとき、
のとき、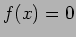 となるのは
となるのは
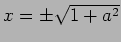 ,
,
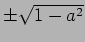 .
そして
.
そして 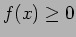 となるのは、
となるのは、
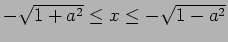 または
または
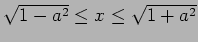 .
.
- (ii)
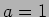 のとき、
のとき、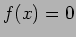 となるのは、
となるのは、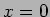 ,
,
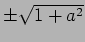 .
そして
.
そして 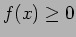 となるのは、
となるのは、
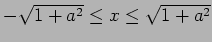 .
.
- (iii)
-
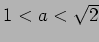 のとき、
のとき、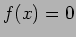 となるのは
となるのは
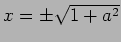 .
そして
.
そして 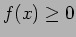 となるのは、
となるのは、
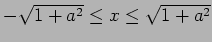 .
(参考:
.
(参考: 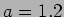 の場合のグラフ)
の場合のグラフ)
- (3)
-
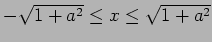 ,
,
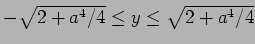 の
範囲に存在する。
の
範囲に存在する。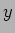 軸との交点は
軸との交点は
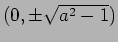 .
.


Next: この文書について...
Up: 平面曲線
Previous: 6.11 アステロイド
Masashi Katsurada
2011-10-01
![]() 平面上で、
方程式
平面上で、
方程式
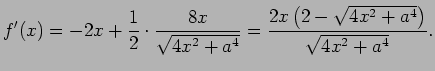
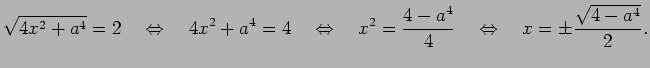
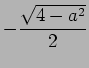
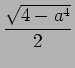
![\includegraphics[width=6cm]{cassini/graph1.eps}](img177.png)
![\includegraphics[width=6cm]{cassini/graph2.eps}](img181.png)
![\includegraphics[width=6cm]{cassini/graph3.eps}](img183.png)
![\includegraphics[width=10cm]{cassini/graph.eps}](img186.png)