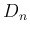5 Dirichlet 核 $D_n$ のグラフを描いてみる

Fourier級数の 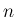$n$ 項までの部分和

$$s_n(x)=\frac{a_0}{2}+\sum_{k=1}^n\left(a_k\cos kx+b_k\sin kx\right) =\sum_{k=-n}^n c_k e^{ikx}$$

は、

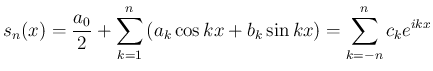
$$D_n(x):=\sum_{k=-n}^{n}e^{ikx}=\frac{\sin\left[(n+1/2)x\right]}{\sin(x/2)}$$

を用いて

$$s_n=D_n\ast f$$

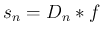
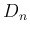と表示することが出来る。$D_n$ は Dirichlet 核と呼ばれる。

Mathematica でお絵描き (検算も兼ねて)

Di[n_,x_]:=Sin[(n+1/2)x]/Sin[x/2];
Di2[n_,x_]:=Sum[Exp[I k x],{k,-n,n}];
g=Plot[{Di[4_,x_],Di2[4,x]},{x,-3Pi,3Pi}]

Figure 1: Dirichlet 核 $D_n$ のグラフ ($n=4$ の場合)