3 Mathematica で離散 Fourier 変換

Mathematica の関数 Fourier[] は、 c=Fourier[f] とすると、 数値のリスト f 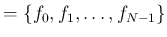$=\{f_0,f_1,\dots,f_{N-1}\}$ に対して

$$C_n:= \frac{1}{\sqrt{N}}\sum_{j=0}^{N-1} f_j\omega^{nj}$$   ( $n=0,1,\cdots,N-1$)

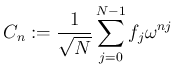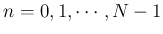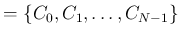を並べたリスト c $=\{C_0,C_1,\dots,C_{N-1}\}$ を返す (これが Mathematica の離散 Fourier 変換の定義)。 逆変換は InverseFourier[c] で行なう。

可能な場合は高速 Fourier 変換を使って計算されるので、 効率が良くなる (効率をあげたいときは 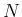$N$ の値に注意すべきである)。

この講義の離散 Fourier 変換の定義に一致する結果を得るには、 次のようなオプションを指定する。

Fourier[f,FourierParameters->{-1,-1}]

逆離散Fourier変換するための関数 InverseFourier[] がある。 この関数でも同じオプション FourierParameters->{-1,-1}] が有効である。

t2=InverseFourier[Fourier[t]] とすると、 t と t2 は等しくなるはずだが、 実際には丸め誤差が発生するので等しくならないことが多い。 丸め誤差のため、 t が実数値であっても、t2 は実数値とは限らない。 ListPlay[] は虚数データを再生出来ないので

t2=Re[InverseFourier[Fourier[t]]]

のように Re[] (実部を求める操作) を施す必要があるかもしれない。