授業の訂正
桂田 祐史
Date: 2017年9月2x日〜
授業中の間違いのうち、授業の後から気づいたものを記録することにしています。
変だなと思ったら、なるべく授業中に指摘・質問して下さい。
- 2017/10/4 授業の終盤
の証明で不等式の向きを間違えました (泣)。
証明.
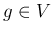
として、
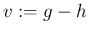
とおく (
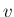
は
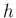
から
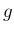
に向かうベクトル)。
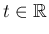
に対して、
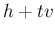
は
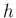
と
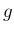
を結ぶ直線 (
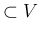
) 上を動く。
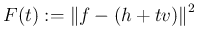
(
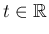
)
という関数を考える。
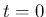
のとき、
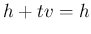
で、
これが
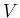
上の点のうち最も
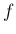
に近いという仮定から、
つまり
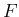
は
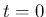
で最小である。
は2次関数であるから、
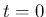
で最小であるためには
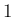
次の係数が
0
でなけれ
ばならない。
これが任意の
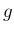
について成り立つことから、
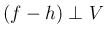
.


桂田 祐史
2017-10-04