Next: 11 線積分の験算 Up: 複素数と Mathematica Previous: 9 複素対数関数を描く
冪級数
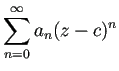 が収束円周上のある点
が収束円周上のある点 ![]() で
収束するならば、その冪級数は “Stolzの角領域” で一様収束するので、
和はそこで連続な関数である、というのが Abel の連続性定理で、
それにより、
で
収束するならば、その冪級数は “Stolzの角領域” で一様収束するので、
和はそこで連続な関数である、というのが Abel の連続性定理で、
それにより、
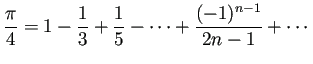
例えば ![]() ,
, ![]() の場合、
の場合、
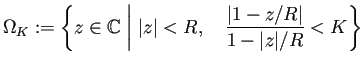
stolz[K_, R_] :=
Block[{g1, g2},
g1 = ContourPlot[x^2 + y^2 == R^2, {x, -2 R, 2 R}, {y, -2 R, 2 R}];
g2 = RegionPlot[
x^2 + y^2 < R^2 &&
Abs[1 - (x + I y)/R]/(1 - Abs[x + I y]/R) <= K, {x, -2 R,
2 R}, {y, -2 R, 2 R}]; Show[g1, g2]
]
R=1
Manipulate[stolz[K,R],{K,1,10,0.2}]
|
筆者は、Mathematica を使うまで、![]() がどういう形をしているか、
実は良く分かっていなかった
(そんなに難しくもないけれど、ちょっと考えて分かるものでもなくて、
何となく気になってはいたけれど、放置していました。)。
がどういう形をしているか、
実は良く分かっていなかった
(そんなに難しくもないけれど、ちょっと考えて分かるものでもなくて、
何となく気になってはいたけれど、放置していました。)。