Next: 9 複素対数関数を描く Up: 複素数と Mathematica Previous: 7 部分分数分解
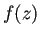
人手で解く場合は、まず ![]() を部分分数に分解する。
そのためには、
を部分分数に分解する。
そのためには、
![]() を
を ![]() で割りたくなる。
で割りたくなる。
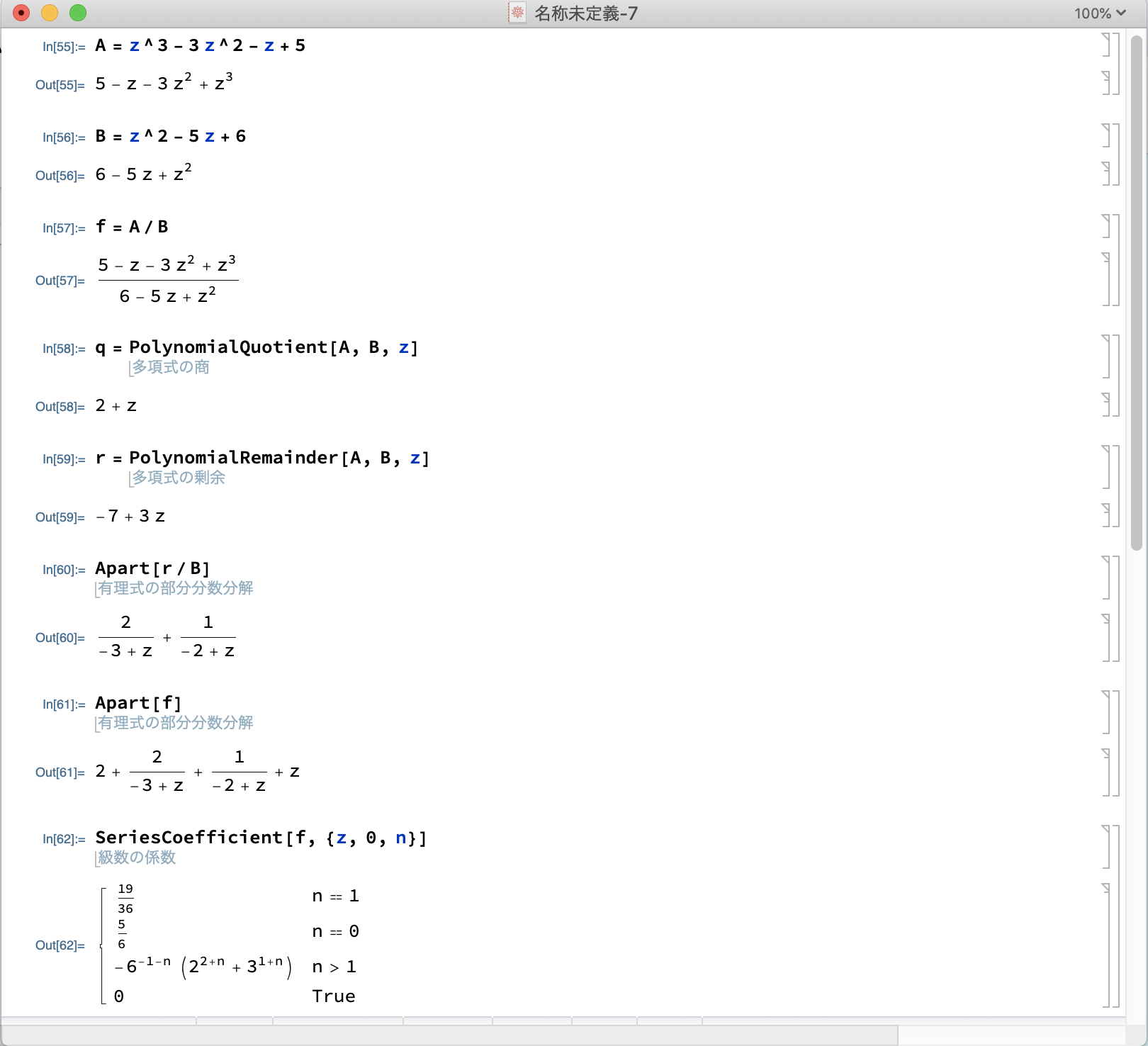
A=z^3-3z^2-z+5 B=z^2-5z+6 f=A/B q=PolynomialQuotient[A,B,z] r=PolynomialRemainder[A,B,z] |
{q,r}=PolynomialQuotientRemainder[A,B,z]
|
これから商 ![]() , 余り
, 余り ![]() が求まる
(商は quotient, 余りは remainder.
polynomial は多項式という意味)。ゆえに
が求まる
(商は quotient, 余りは remainder.
polynomial は多項式という意味)。ゆえに
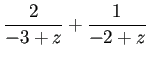
Apart[r/B] Apart[f] |
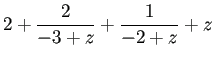 ,
,
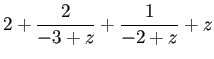 となる。
となる。
結局
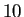
Series[f,{z,0,10}] とすると、
0 の周りの Taylor 展開を ![]() 次の項まで求めることが出来る。
次の項まで求めることが出来る。
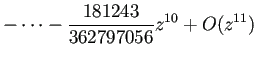 (途中省略)
(途中省略)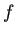
0 の周りのTaylor展開の第![]() 項は
項は
SeriesCoefficient[f,{z,0,n}]
|
![]() の 0 の周りの Taylor 展開は
の 0 の周りの Taylor 展開は
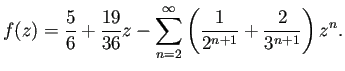
Sum[] で検算が可能で、
5/6+19z/36-Sum[(1/2^(n+1)+2/3^(n+1))z^n,{n,2,Infinity}]
Simplify[%]
|