単位円版
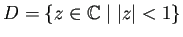 の写像関数、
つまり双正則な
の写像関数、
つまり双正則な
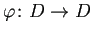 は、
は、
に限ることを示せ。
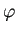 が1次分数変換の場合にこの形になることは授業で説明する予定であるが、
より一般に
が1次分数変換の場合にこの形になることは授業で説明する予定であるが、
より一般に 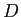 から
から 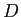 への双正則な写像とした場合でも、
(2) の形の写像しかないことは有名な結果である
(それによって1次分数変換の重要性の理解が深まる)。
少し程度の高い関数論のテキストには載っていることが多いので、
それを読んで理解した上でまとめること。
Schwarz の補題 (これも有名な定理) を用いる場合は、その証明も含めること。
への双正則な写像とした場合でも、
(2) の形の写像しかないことは有名な結果である
(それによって1次分数変換の重要性の理解が深まる)。
少し程度の高い関数論のテキストには載っていることが多いので、
それを読んで理解した上でまとめること。
Schwarz の補題 (これも有名な定理) を用いる場合は、その証明も含めること。
(等角写像と1次分数変換については、授業で時間切れになるので、
有名な結果を自習してみたらいかがでしょう、という主旨。
載っているテキストが自分で見つけられなかったら質問してください。
Maruzen eBook Library で閲覧できる本の中にも紹介できる本があるので、
図書館に足を運ばなくても何とかなります。)
桂田 祐史