Riemann のゼータ関数 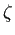 を複数の方法で可視化せよ
(実関数のグラフ、実部・虚部・絶対値などのグラフや等高線)。
を複数の方法で可視化せよ
(実関数のグラフ、実部・虚部・絶対値などのグラフや等高線)。
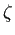 は
は
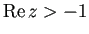 の範囲ならば
の範囲ならば
|
(1) |
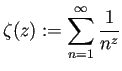 (ただし (ただし
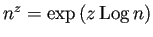 ) ) |
で定義されるが (桂田[1]の例2.12)、
解析接続によってより広い領域まで拡張される
(それについてレポート中で説明すれば加点する)。
Mathematica であれば Zeta[] で、
Python であれば mpmath.zeta() で、
MATLAB であれば zeta() で計算できる。
(Riemannのゼータ関数は、数学好きならば知っている可能性の高い有名人
(有名な関数) である。
数学系ソフトウェアの多くで計算が容易になっているので、
気軽に触れることができる。ではやってみよう、という主旨である。)
桂田 祐史