Next: 2.1.2 Runge гҒ®зҸҫиұЎ Up: 2.1 иЈңй–“еӨҡй …ејҸ Previous: 2.1 иЈңй–“еӨҡй …ејҸ
![\begin{jproposition}[иЈңй–“еӨҡй …ејҸгҒ®дёҖж„ҸеӯҳеңЁ]
$[a,b]$ гҒҜ $\mathbb{R}$\...
...Ғҷе®ҹдҝӮж•°еӨҡй …ејҸ $f_n(x)$ гҒҢдёҖж„Ҹзҡ„гҒ«еӯҳеңЁгҒҷгӮӢгҖӮ
\end{jproposition}](img28.png)
|
| (3) | 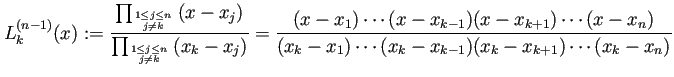 |
| (4) |
| (5) | 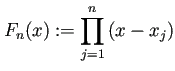 |
| (6) | 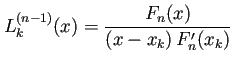 |
| (7) | 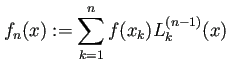 |
д»ҘдёҠгҒ§еӯҳеңЁгҒҢзӨәгҒӣгҒҹгҖӮ![]() ж¬ЎеӨҡй …ејҸгҒ®дҝӮж•°
ж¬ЎеӨҡй …ејҸгҒ®дҝӮж•°
![]() (гҒӨгҒҫгӮҠ
(гҒӨгҒҫгӮҠ
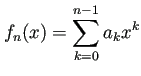 гҒЁгҒ„гҒҶгҒ“гҒЁ)
гӮ’
гҒЁгҒ„гҒҶгҒ“гҒЁ)
гӮ’ ![]() ,
, ![]() ,
, ![]() ,
, ![]() гҒ§гҒ®еҖӨ
гҒ§гҒ®еҖӨ ![]() ,
, ![]() ,
,
![]() ,
, ![]() гӮ’еҜҫеҝңгҒ•гҒӣгӮӢеҶҷеғҸгҒҜгҖҒ
гӮ’еҜҫеҝңгҒ•гҒӣгӮӢеҶҷеғҸгҒҜгҖҒ
![]() гҒӢгӮү
гҒӢгӮү
![]() гҒёгҒ®з·ҡеһӢеҶҷеғҸгҒ§гҒӮгӮӢгҖӮ
дёҠгҒ§гҒқгӮҢгҒҢе…Ёе°„гҒ§гҒӮгӮӢгҒ“гҒЁгҒҢеҲҶгҒӢгҒЈгҒҹгҖӮ
з·ҡеҪўд»Јж•°гҒ§еӯҰгҒ¶е®ҡзҗҶгҒ«гӮҲгҒЈгҒҰгҖҒгҒқгӮҢгҒҜеҚҳе°„гҒ§гҒӮгӮӢгҖӮ
гҒ“гӮҢгҒҜ
гҒёгҒ®з·ҡеһӢеҶҷеғҸгҒ§гҒӮгӮӢгҖӮ
дёҠгҒ§гҒқгӮҢгҒҢе…Ёе°„гҒ§гҒӮгӮӢгҒ“гҒЁгҒҢеҲҶгҒӢгҒЈгҒҹгҖӮ
з·ҡеҪўд»Јж•°гҒ§еӯҰгҒ¶е®ҡзҗҶгҒ«гӮҲгҒЈгҒҰгҖҒгҒқгӮҢгҒҜеҚҳе°„гҒ§гҒӮгӮӢгҖӮ
гҒ“гӮҢгҒҜ ![]() гҒҢдёҖж„Ҹзҡ„гҒ«е®ҡгҒҫгӮӢгҒ“гҒЁгӮ’ж„Ҹе‘ігҒ—гҒҰгҒ„гӮӢгҖӮ
гҒҢдёҖж„Ҹзҡ„гҒ«е®ҡгҒҫгӮӢгҒ“гҒЁгӮ’ж„Ҹе‘ігҒ—гҒҰгҒ„гӮӢгҖӮ ![]()
![]()
![]() ,
, ![]() ,
,
![]() гӮ’гҖҒ
гӮ’гҖҒ
![]() ,
, ![]() ,
, ![]() гӮ’жЁҷжң¬зӮ№гҒЁгҒҷгӮӢ Lagrange иЈңй–“дҝӮж•°гҒЁе‘јгҒ¶гҖӮ
гӮ’жЁҷжң¬зӮ№гҒЁгҒҷгӮӢ Lagrange иЈңй–“дҝӮж•°гҒЁе‘јгҒ¶гҖӮ
дёҠгҒ®е®ҡзҗҶгҒ® ![]() гӮ’
гӮ’ ![]() гҒ®иЈңй–“еӨҡй …ејҸ (interpolating
polynomial) гҒЁе‘јгҒ¶гҖӮ
дёҠгҒ®иӯ°и«–гҒӢгӮүеҲҶгҒӢгӮӢгӮҲгҒҶгҒ«
гҒ®иЈңй–“еӨҡй …ејҸ (interpolating
polynomial) гҒЁе‘јгҒ¶гҖӮ
дёҠгҒ®иӯ°и«–гҒӢгӮүеҲҶгҒӢгӮӢгӮҲгҒҶгҒ«
| (8) | 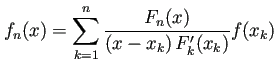 |
(NewtonгҒ®иЈңй–“е…¬ејҸ (Newton иЈңй–“еӨҡй …ејҸ, Newton polynomial) гҒЁгҒ„гҒҶгӮӮгҒ®гӮӮгҒӮгӮӢгҒҢгҖҒ иЈңй–“еӨҡй …ејҸгҒ§гҒӮгӮӢгҒ“гҒЁгҒ«гҒҜеӨүгӮҸгӮҠгҒҢгҒӘгҒ„гҖӮ)
жЎӮз”° зҘҗеҸІ