Next: 2.2 Poisson方程式に対する弱解の方法 Up: 2.1 ポテンシャル問題に対する解の存在証明、Dirichletの原理 Previous: 2.1 ポテンシャル問題に対する解の存在証明、Dirichletの原理
![$\displaystyle J[u]=\dint_\Omega\left(u_x^2+u_y^2\right)\DxDy$](img29.png) (この
(この
![$\displaystyle f(t)=J[u]+2t\dint_\Omega\left(u_x v_x+u_y v_y\right)\DxDy
+t^2\dint_\Omega\left(v_x^2+v_y^2\right)\DxDy
$](img39.png)
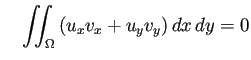
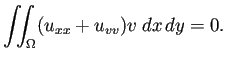
以上の議論から、
![]() を最小にするような
を最小にするような ![]() を見出せば問題が解決することが分かる。
を見出せば問題が解決することが分かる。
![]() は常に
は常に ![]() を満たすので、
を満たすので、![]() が下に有界でありることは明らかで、
従って
が下に有界でありることは明らかで、
従って ![]() の下限が存在する。
Riemann は、
(この下限は最小値であるから) 最小値を与える
の下限が存在する。
Riemann は、
(この下限は最小値であるから) 最小値を与える ![]() が存在する、と議論したのだが、
Weierstrass は「下限は最小値である」ことに疑義を示した
(「数学解析」を学んだ人は、
いかにも Weierstrass がツッコミそうなところと思うかも)。
が存在する、と議論したのだが、
Weierstrass は「下限は最小値である」ことに疑義を示した
(「数学解析」を学んだ人は、
いかにも Weierstrass がツッコミそうなところと思うかも)。 ![]()
残念ながら若くして亡くなった Riemann は、 Weierstrass の批判に答えることが出来なかった。 この論法による完全な証明は、 約 50 年後 (1900年頃) に D. Hilbert が解決するまで持ち越された。
本当は、Dirichlet の原理は、 C. F. Gauss (1777-1855) がルーツで、 物理学の世界ではすでに知られていた考え方で、 それを Riemann が純粋数学に応用したのだ、という見方をする人もいる。