3.1 FreeFem++ プログラム (その1)

有限要素法は、弱解の方法を原理とする数値計算法である。 それはプログラム作成のかなりの部分を自動化出来るため、 専用のソフトウェアがいくつか開発されている。

その1つである、 FreeFem++ は、 パリ第6大学 J. L. Lions 研究所の Frédéric Hecht, Oliver Pironneau, A. Le Hyaric, 広島国際学院大学の大塚厚二氏らが開発した、 2次元, 3次元問題を有限要素法で解くための、 一種の PSE (problem solving environment) である。 ソースコード、マニュアル (約400ページ, 幸い英文)、 主なプラットホーム (Windows, Mac, Linux) 向けの 実行形式パッケージが公開されている。

細かいことは、以前書いた桂田 [1] という紹介文を見てもらうことにする。

有限要素法の定番教科書の一つである菊地 [3] に載っている Poisson 方程式の例題

$$-\Laplacian u=f \mbox{in $\Omega$} ,$$ (3.1)

$$u=g_1 \mbox{in $\Gamma_1$} ,$$ (3.2)

$$\frac{\rd u}{\rd n}=g_2 \mbox{in $\Gamma_2$}$$ (3.3)

(ただし、 $\Omega=(0,1)\times(0,1)$, $\Gamma_1=\{0\}\times[0,1]\cup [0,1]\times\{0\}$, $\Gamma_2=\{1\}\times(0,1]\cup(0,1]\times\{1\}$, $f=1$, $g_1=0$, $g_2=0$) を FreeFEM++ を用いて解くとどうなるか。

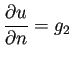次のようなプログラムで解ける。

Poisson2.edp

// Poisson2.edp
int Gamma1=1, Gamma2=2;
border Gamma10(t=0,1) { x=0; y=1-t; label=Gamma1; }
border Gamma11(t=0,1) { x=t; y=0; label=Gamma1; }
border Gamma20(t=0,1) { x=1; y=t; label=Gamma2; }
border Gamma21(t=0,1) { x=1-t; y=1; label=Gamma2; }
int m=10;
mesh Th = buildmesh(Gamma10(m)+Gamma11(m)+Gamma20(m)+Gamma21(m));
plot(Th, wait=1,ps="Th.eps");
savemesh(Th,"Th.msh"); // optional
fespace Vh(Th,P1);
Vh u,v;
func f=1;
func g1=0;
func g2=0;
solve Poisson(u,v) =
   int2d(Th)(dx(u)*dx(v)+dy(u)*dy(v))
  -int2d(Th)(f*v)
  -int1d(Th,Gamma2)(g2*v)
  +on(Gamma1,u=g1); // on(Gamma10,Gamma11,u=g1) 
plot(u,ps="contour.eps");

プログラムはテキスト・エディター (現象数理学科 Mac では、 mi, テキスト・エディット⁴, emacs など) で作成し、ターミナルから、

こんなふうにして実行

FreeFem++ Poisson2.edp

とタイプして実行できる。 キーを打つごとに次の図に移り、 最後は キーを打って終了する。

図 1: Poisson2.edp の出力 -- 要素分割と解の等高線