応用複素関数レポート課題3
桂田 祐史
Date: 2019年7月22日 :
この科目はあまりシビアに成績をつけようとは思っていません。
課題1,2を普通に解いておけば良いです。
課題1,2のどちらかを提出し損なったとか、
あまり良いレポートが書けなかったので挽回の機会が欲しい、
と言う人がいたので、(主に)彼ら向けに追加の課題を出します。
締め切りは8月2日(金曜)18:00とします。Oh-o! Meiji で提出して下さい。
自分で勉強・実験する意味があると考えることをやってもよいです
(不安だったら、「こんなことをしようと思っているけれど、
それで良いでしょうか」と尋ねて下さい)。
- Jordan領域の等角写像を、
ポテンシャル問題を解いて求めるアルゴリズムの紹介をしました
(桂田 [1])。
それを実行して等角写像を求めてみる。
[1]には、
C++で書いたプログラムが載っていますが、
別のプログラミング言語でやってみるとか。
一度プログラムが動き出すと、色々な Jordan 領域で試せるはずです
([1] のプログラムでは、
単位円盤の場合を計算するようになっています)。
- 級数の話を留数計算で求める話をしました
(7月1日の授業, 桂田 [2] の §1.3)。
何か本に載っていない実例を自分で計算してみて下さい。
一部 Mathematica を利用しても構いません。
何らかの意味で検算をして下さい。
- Euler による公式
を紹介するだけで証明が出来なかったのを残念に思っています
(7月8日の授業, 桂田 [2] の §5)。
自分なりに証明をまとめてみるとか。
数値計算で確認できるか考えてみるとか。
- (これは以前出題したことがあるけれど、あまりうまく解けた人がいません。)
Eulerの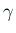 定数
定数
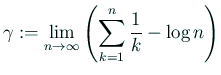 は
は
という積分表現が出来ることが知られています。
これを数値積分することで 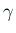 の値を計算して下さい。
(被積分関数
の値を計算して下さい。
(被積分関数
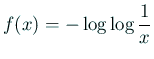 がどういう関数か調べて、
適切な数値積分公式を選んで、注意深く計算する必要があります。)
がどういう関数か調べて、
適切な数値積分公式を選んで、注意深く計算する必要があります。)
- (これも以前出題したことがあるけれど、あまりうまく解けた人がいません。)
Euler の
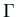 関数
関数
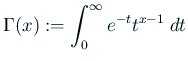 (
(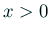 ) を、数値積分を利用して計算する
プログラムを作り、どの程度の精度が得られるか、調べて下さい。
(やはり
) を、数値積分を利用して計算する
プログラムを作り、どの程度の精度が得られるか、調べて下さい。
(やはり
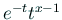 がどのような関数か調べることが大事です)。
がどのような関数か調べることが大事です)。
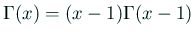 などの公式は利用して構いません。
などの公式は利用して構いません。
- これは本日 (7月22日) の授業の話ですが
(桂田 [3] の§6,
§G に Mathematicaプログラムが載っています)、
数値積分公式の誤差の特性関数
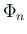 の絶対値の等高線を描いてみて下さい。
台形公式、中点公式、Simpson公式の誤差の特性関数の比較、とか。
の絶対値の等高線を描いてみて下さい。
台形公式、中点公式、Simpson公式の誤差の特性関数の比較、とか。
(数値計算法の良し悪しのデモンスレーションとして、
特定の問題に適用した時の精度を見せたりするのはよくあるけれど、
計算法固有の性質を “可視化” して見せたのは、
よくそんなことが出来たものだ、すごい、と今さらながら感心します。)
桂田 祐史
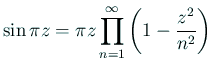
![]() 定数
定数
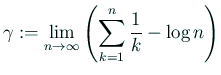 は
は
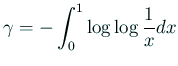
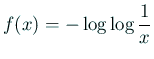 がどういう関数か調べて、
適切な数値積分公式を選んで、注意深く計算する必要があります。)
がどういう関数か調べて、
適切な数値積分公式を選んで、注意深く計算する必要があります。)
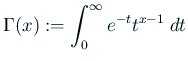 (
(