Next: おまけ Up: 応用複素関数レポート課題3 Previous: 応用複素関数レポート課題3
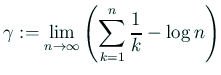 で定義されるが、この式で
で定義されるが、この式で 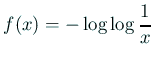 がどういう関数か調べて、
注意して計算すること。)
結果を何らかの方法でチェックすること。
(1) がなぜ成り立つか調べることが望ましい。
がどういう関数か調べて、
注意して計算すること。)
結果を何らかの方法でチェックすること。
(1) がなぜ成り立つか調べることが望ましい。
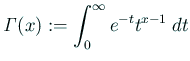 (
(
(注) よく知られている関数等式
![]() を利用すると、
どこか都合の良い幅
を利用すると、
どこか都合の良い幅 ![]() の区間に属する
の区間に属する ![]() に対して数値積分で
に対して数値積分で
![]() を求めれば良いことになる。
を求めれば良いことになる。
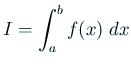 に対する数値積分公式では、
に対する数値積分公式では、
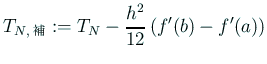
がある。台形公式
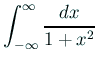 に対しては、
変数変換
に対しては、
変数変換
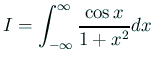 (値は
(値は 参考: 大浦氏自身の作成した DE 公式のプログラムが、 http://www.kurims.kyoto-u.ac.jp/~ooura/index-j.htmlで公開されている (intde2.c)。 「この論文はどうすれば手に入るか?」という質問はいつでも受け付ける (メール下さい)。