Next: 5.1.2 Poisson 方程式の特解 Up: 5.1 準備 Previous: 5.1 準備
![]() 次元の場合
次元の場合
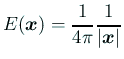 ,
,
![]() 次元の場合
次元の場合
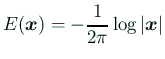 を
を
![]() の基本解 (the fundamental solutionn) と呼ぶ。
の基本解 (the fundamental solutionn) と呼ぶ。
![]() は原点以外では調和関数であることは簡単な計算で分かる:
は原点以外では調和関数であることは簡単な計算で分かる:
さらに、超関数の言葉で言うと (原点まで込めて)
| (5.1) |
物理的な解釈:
原点に置かれた単位点電荷の作る電場のポテンシャルが ![]() である。
である。
桂田 祐史