Next: 2 ポテンシャル問題に対する Dirichletの原理と Poisson Up: ポテンシャル問題とその数値解法 Previous: 目次
Laplace 方程式
![]() の境界値問題をポテンシャル問題という。
正則関数の実部・虚部は調和関数 (ラプラス方程式の解) であるため、
関数論のあちこちの重要な場面でポテンシャル問題が登場する。
例えば関数論で重要な定理の一つである Riemannの写像定理に現れる
等角写像を求めるためにも、ポテンシャル問題が現れる。
の境界値問題をポテンシャル問題という。
正則関数の実部・虚部は調和関数 (ラプラス方程式の解) であるため、
関数論のあちこちの重要な場面でポテンシャル問題が登場する。
例えば関数論で重要な定理の一つである Riemannの写像定理に現れる
等角写像を求めるためにも、ポテンシャル問題が現れる。
(2次元渦無し非圧縮流の速度ポテンシャル ![]() は、
Laplace 方程式のNeumann境界値問題
は、
Laplace 方程式のNeumann境界値問題
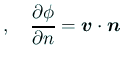 on
on
の解である、ということを既に紹介したが、 そのような応用上の問題に止まらない、ということを認識してもらいたい。)
ここでは少し一般化した Poisson 方程式の境界値問題
実は、この問題は非常に筋の良い問題であり、 様々な数値計算法が適用出来る。 ここでは、(1) 差分法, (2) 有限要素法, (3) 基本解の方法を紹介する。
差分法、有限要素法は、偏微分方程式に対する数値解法の、 二大スタンダードと言えるもので、 そういう有名な方法を紹介出来るのは有意義と考えられる。 基本解の方法は、微分作用素の簡単な基本解が分かっているという、 Laplace 方程式の特徴を最大限に生かす方法で、 Laplace方程式の解法としては特に優れていると言える。
桂田 祐史