2.3.2 滑らかな関数の場合

$I=\dsp\int_0^1 e^x\;\Dx$

/*
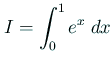
 * example2.c -- \int_0^1 e^x dx
 *   cc example2.c
 *   ./a.out > ex2.data
 */

#include <stdio.h>
#include <math.h>
#include "nc.c"

double f(double x)
{
  return exp(x);
}

int main(void)
{
  int N;
  double a, b, If;
  double  M, T, S;
  a = 0.0; b = 1.0; If = exp(1.0) - 1;
  printf("#   N       I-M_N           I-T_N         I-S_N\n");
  for (N = 2; N <= 65536; N *= 2) {
    M = midpoint(f, a, b, N);
    T = trapezoidal(f, a, b, N);
    S = simpson(f, a, b, N);
    printf("%5d  %14e %14e %14e\n", N, If - M, If - T, If - S);
  }
  return 0;
}

$ cc -o example2 example2.c
$ ./example2

(結果は自分でやってみよう)

$ ./example2 > ex2.data
$ gnuplot example2.gp -

(結果は図 2)

グラフの横軸は $N$ (標本点数$-1$ )、縦軸は誤差 (いずれも対数目盛) である。 $\qedsymbol$

図: $\dsp I=\int_0^1 e^x\;\Dx$ を中点公式、 台形公式、Simpson公式で計算したときの誤差

事実2

     滑らかな関数に対して、

$$I-M_N=O\left(\frac{1}{N^2}\right),\quad I-T_N=O\left(\frac{1}{N^2}\right),\quad I-S_N=O\left(\frac{1}{N^4}\right).$$

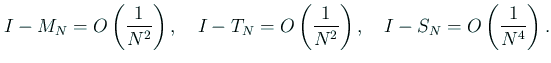
高次の公式の方が収束は速い or 等しい。 必ず速いわけでなく、等しい場合もある (台形公式が中点公式より優れているわけではない)。 実は、これは公式の位数とも関係する。