Next: 3.3 正則関数の定める流れを Mathematica で可視化 Up: 3.2 簡単な流れ Previous: 3.2.2 湧き出し、吸い込み
(上の ![]() の
の ![]() を純虚数に変えてみる。)
を純虚数に変えてみる。)
![]() ,
,
![]() (
(
![]() ) の場合。
) の場合。
![]() とすると、
とすると、
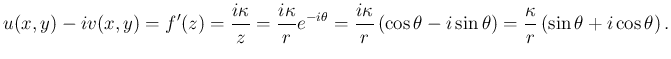
すなわち
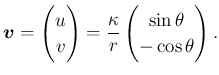
(
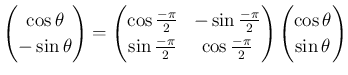 であるから、
であるから、
速度ポテンシャルと流れ関数は、
![]() (
(
![]() ) より
) より
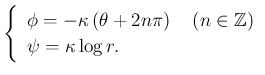
流線は原点を中心とする円で、 等ポテンシャル線は原点を端点とする半直線である。
原点に置かれた渦糸 (渦点) の流れと呼ばれる。
渦度は
![]() 全体で 0
であることに注意しよう。
全体で 0
であることに注意しよう。
桂田 祐史