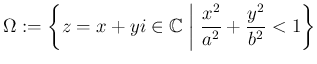2 レポート課題 part 1
締め切りは7月21日19:30 (以前18:00と言いましたが、
ゼミをやっている時間で、中途半端であると言われたので、
少しずらしました), 提出方法は Oh-o! Meiji.
もし容量制限に引っかかった場合は、早目にメールで相談して下さい。
(FreeFem++ がうまくインストール出来ない、という場合も相談に乗りますが、
〆切が近づくとこちらも忙しいので、早目早目でお願いします。)
以下 [1]〜[5] から1つ以上解いて下さい。
使用するプログラミング言語の選択は基本的に自由ですが、
桂田が相談に乗るためには、
自分の MacBook Air で実行して見せてもらう必要があります1。
- [1]
- 正則関数の定める流れ (Mathematica を使うことを想定)
- (1)
- 渦糸の等ポテンシャル線、流線、
ベクトル場を適当に (流れの様子が良く分かるように) 可視化する。
(湧き出しのサンプル・プログラムはあるので簡単のはず。
追記 プログラムは、
講義内容と対応するように書かれていて、
きちんと解読すること。
もちろん細かいところは問題に合うように書き換える必要がある。)
- (2)
- 自分で思いつく正則関数を5つ以上試し
(「 係数だけを変えて数合わせ」ではなく、なるべく「違う」ものを選ぶこと)、
そのうちの1つを選んで、
それを複素速度ポテンシャルとする流れについて、
等ポテンシャル線、流線、
ベクトル場を適切に可視化し、
それをもとにどういう流れであるか説明する
(流量の計算をしてみるとか…)。
正則関数の実部・虚部の等高線自体は、関数論のテキストの多くに載っている。
凝りたければ、今井 [2] 等を見て関数を選ぶと良い。
追記 「簡単な流れの合成」という話をしてある。
それや初等関数の定める流れを描いてみることを授業で勧めた。
- [2]
- ポテンシャル問題を解くことによる流れの決定 (FreeFem++ を使うことを想定)
2次元渦なし非圧縮の定常流で、
流体の占める領域の境界での流速が分かっている場合に、
速度ポテンシャル 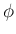 、流れ関数
、流れ関数 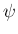 を計算して、
等ポテンシャル線, 流線, ベクトル場を可視化せよ。
--
を計算して、
等ポテンシャル線, 流線, ベクトル場を可視化せよ。
-- 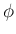 は
は
の解として求まる。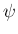 はどうすれば良いか?
(念のため注意: 講義で説明したように、
解
はどうすれば良いか?
(念のため注意: 講義で説明したように、
解 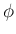 が存在するためには
が存在するためには
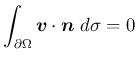 が必要である。
が必要である。
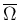 で定義された
で定義された 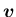 で
で
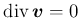 を満たすものはこの条件を満たすが、
を満たすものはこの条件を満たすが、
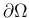 の上だけで
の上だけで 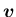 を与える場合は注意すること。)
を与える場合は注意すること。)
- [3]
- 差分法による Poisson 方程式の解法 (1) (MATLAB を使うことを想定)
こちらが提示した MATLAB のサンプル・プログラムは、
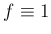 ,
,
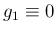 という特殊な場合に
という特殊な場合に
を解くものであるが、
これをより一般の条件のもとで解けるようにプログラムを拡張する。
そのプログラムを別のプログラミング言語 (例えば Python) に移植出来たら加点する。
- [4]
- 差分法による Poisson 方程式の解法 (2)
Poisson 方程式の Neumann 境界値問題、すなわち
の解が存在するためには、
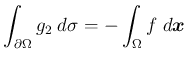 という条件が必要であり、
解が存在するときも解の一意性は成立しない
(
という条件が必要であり、
解が存在するときも解の一意性は成立しない
(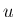 に任意の定数を加えたものはまた解になるから)。
この事情は、離散化して作った差分方程式
に任意の定数を加えたものはまた解になるから)。
この事情は、離散化して作った差分方程式
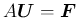 でも変わらない。
でも変わらない。
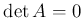 となっているため、解が存在するためには
となっているため、解が存在するためには 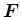 に条件が必要で、
解が存在する場合も一意性は成立しない
(分からなければ線型代数を復習すること)。
この問題を解決し、差分解を求めるプログラムを作る。
1次元、すなわち
に条件が必要で、
解が存在する場合も一意性は成立しない
(分からなければ線型代数を復習すること)。
この問題を解決し、差分解を求めるプログラムを作る。
1次元、すなわち
の場合で構わない。講義では、
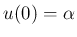 ,
,
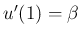 という問題に対して、
行列
という問題に対して、
行列 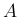 を与えてあるので、それをたたき台にして考察すると良い
(なお、プログラムも C で書いたものを提供してある
http://nalab.mind.meiji.ac.jp/~mk/complex2/potential/node5.html)。
を与えてあるので、それをたたき台にして考察すると良い
(なお、プログラムも C で書いたものを提供してある
http://nalab.mind.meiji.ac.jp/~mk/complex2/potential/node5.html)。
この問題に対して、
``いい加減な'' アプローチをしているプログラムが結構ある。
実は、この講義で提供している FreeFem++ のプログラムもそうである (笑)。
一度じっくり考えてみる価値のある問題である。
- [5]
- (基本解の方法に関する課題)
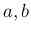 を
を 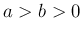 を満たす実数とするとき
を満たす実数とするとき
とおく (つまり、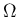 は楕円領域である)。
は楕円領域である)。
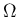 の等角写像
の等角写像
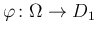 を、
基本解の方法を用いて求めよ。
(もし、厳密解を文献で見つけて、それを計算する方法が得られたら、
上で計算した解と比べて見よ。)
を、
基本解の方法を用いて求めよ。
(もし、厳密解を文献で見つけて、それを計算する方法が得られたら、
上で計算した解と比べて見よ。)
桂田 祐史
2017-08-11
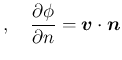 on
on 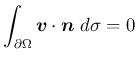 が必要である。
が必要である。
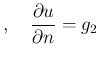 on
on 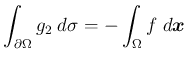 という条件が必要であり、
解が存在するときも解の一意性は成立しない
(
という条件が必要であり、
解が存在するときも解の一意性は成立しない
(