

Next: 2 簡単な流れの可視化
Up: 数値計算実習
Previous: 数値計算実習
(書きかけ)
締め切りは8月1日18:00, 提出方法は Oh-o! Meiji.
複数のファイルを送りたい場合は、zip でまとめて送って下さい。
もし容量制限に引っかかった場合は、早目にメールで相談。
以下のいずれかをして下さい。
使用するプログラミング言語の選択は基本的に自由ですが、
こちらが直接相談に乗るためには、
自分の MacBook Air で実行できて、見せることが出来る必要がある。
- [1]
- (1) 湧き出しまたは渦糸の流線・等ポテンシャル線、
ベクトル場を適当に (流れの様子が良く分かるように) 可視化する。
(2) 自分で思いつく正則関数を5つ以上試し、そのうちの1つを選んで、
それを複素速度ポテンシャルとする流れについて、流線、等ポテンシャル、
ベクトル場を適当に可視化し、それをもとにどういう流れであるか説明する。
- [2]
- 渦なし非圧縮の定常流で、流体の占める領域の境界での流速が分かっている場合に、
速度ポテンシャル、流れ関数を有限要素法で計算して、
当ポテンシャル線, 流線, ベクトル場を可視化せよ。
- [3]
- 自分が選んだ単連結領域
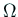 を単位円盤
を単位円盤 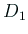 に双正則にうつす写像
に双正則にうつす写像
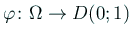 の を基本解の方法を用いて数値的に求めよ。
結果を何らかの方法で確かめること
(もしも真の写像が分かっている場合はそれとの比較、
像が実際に単位円になっていることなど。)。
の を基本解の方法を用いて数値的に求めよ。
結果を何らかの方法で確かめること
(もしも真の写像が分かっている場合はそれとの比較、
像が実際に単位円になっていることなど。)。


Next: 2 簡単な流れの可視化
Up: 数値計算実習
Previous: 数値計算実習
桂田 祐史
2015-07-22