Next: 5.5 上つき添字、下つき添字、それと積分&シグマ Up: 5.4 色々な記号 Previous: 5.4.1 ギリシャ文字
\[
a\in A\subset B,\quad
C\supset D,\quad
a\not\in A,\quad
C\not\supset D,\quad
A\cup B, A\cap B, A\setminus B=\emptyset,\quad
\bigcup_{i=1}^\infty A_i=\bigcap_{i=1}^\infty B_i
\]
|
|
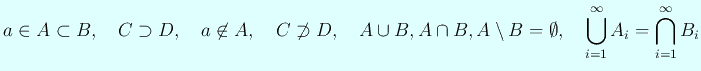
|
![]() (\in) の逆向きが
(\in) の逆向きが
![]() (\ni) であるのは苦し紛れっぽいけど。
(\supset も苦し紛れと思ったのだけれど、
subset の反対語は superset なので、正しい言葉遣いなのだった。)
(\ni) であるのは苦し紛れっぽいけど。
(\supset も苦し紛れと思ったのだけれど、
subset の反対語は superset なので、正しい言葉遣いなのだった。)
包含関係で等号をつけるつけないは、普通の大小関係の不等号 ![]() と同じ感じ。
と同じ感じ。
\[ A\subseteq B,\quad A\subseteqq B,\quad A\subsetneq B,\quad A\subsetneqq B. \] |
|
|
論理の記号:
and ![]() は \wedge,
or
は \wedge,
or ![]() は \vee,
not
は \vee,
not ![]() は \neg とする。
は \neg とする。
\[ \neg(P\wedge Q)\equiv \neg P\vee \neg Q. \] |
|
|
矢印のところで説明済みだが、
![]() は \Leftrightarrow,
は \Leftrightarrow,
![]() は \Rightarrow
は \Rightarrow
桂田 祐史