Next: 6 文書の構造など Up: 5 簡単な数式 Previous: 5.16 数式番号について
\[
f(x)\stackrel{\mathrm{def.}}{=}x^2+2x+3,\quad
g(x)\overset{\mathrm{def.}}{=}3x^2+2x+1,\quad
h(x)\underset{\mathrm{def.}}{=}\sin x.
\]
|
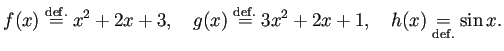
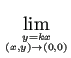 は
上\atop 下 や
\genfrac{}{}{0pt}{1}{上}{下}
は
上\atop 下 や
\genfrac{}{}{0pt}{1}{上}{下}
\[
\lim_{y=kx\atop (x,y)\to(0,0)}\frac{x y}{x^2+y^2}
=
\lim_{\genfrac{}{}{0pt}{1}{y=kx}{(x,y)\to(0,0)}}\frac{x y}{x^2+y^2}
\]
|
|
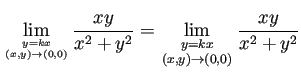
|