Next: 8.4 The Hansen-Bliek-Rohn-Ning-Kearfott-Neumaier Method Up: 8 連立1次方程式 Previous: 8.2 区間Gauss消去法
区間連立1次方程式
![]() は、
行列
は、
行列
![]() をかけることで前処理できる。
ここで
をかけることで前処理できる。
ここで ![]() を、
を、![]() の中点行列 (midpoint matrix) の逆行列と選ぶと、
の中点行列 (midpoint matrix) の逆行列と選ぶと、
![]() はしばしば
はしばしば ![]() -行列となる。
その場合は Gauss の消去法が使えるが、Krawczyk の方法を用いて、
包み込みを計算する方が速い。
-行列となる。
その場合は Gauss の消去法が使えるが、Krawczyk の方法を用いて、
包み込みを計算する方が速い。
区間ベクトル
![]() が解集合を包み込む:
が解集合を包み込む:
![]() と仮定する。
このとき、任意の
と仮定する。
このとき、任意の
![]() ,
,
![]() に対して
に対して
この反復を
![\begin{jtheorem}[]
$C\in\mathbb{R}^{n\times n}$ が$\left\Vert I-C\tilde A\rig...
...c{\left\Vert C\tilde b\right\Vert}{\;1-\beta\;}.
\end{displaymath}\end{jtheorem}](img231.gif)
|
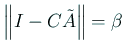 から)
から)
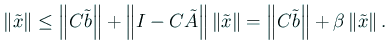
桂田 祐史