脚注

NaN はそういう使い方をするものだろうか？

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...gfpp.mを入手して ²

URL は http://www.math.sjsu.edu/~foster/gfpp.m となる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... と呼び出さねばならない。これは条件数を２乗にすることに注意 ³

うーん、ひょっとして「正定値性のない、ただの対称行列については、第３引数に 1 を指定せよ、でもそうすると、条件数を2乗することになるよ」。中で

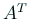でもかけて正値対称にしているのか？と推測するけれど、そうさせるのは、説明がいいかげんだよね。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... を見よ ⁴

「ソースを読め」かな？

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... は次のようになる ⁵

第1段階の7回反復で成功しない場合は、それにつづけて第2段階をするわけで、 t2/t1 に 1 を加えた倍率の時間がかかるわけか。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 現時点での実装は正値対称行列のみ ⁶

(大石先生が時々「疎行列については正値対称の場合のみ出来ている」と言っているのはこのこと？誰がやったと言っていなくて、漠然と大石グループの仕事だと思っていたけれど、実は大石先生が始める前の Rump の古い仕事ということなのか？

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 点行列について残差改良をする ⁷

残差改良というのは…そういえば僕は説明を書いたことがないな。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... に対してのみ行われる ⁸

うーん？？疎行列や区間行列については残差改良はしない、ということか。でも、それは「解釈のオーバーヘッドのため」なのか？？

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 列と点ベクトル、相対誤差は...⁹

英語になってない。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... 「四捨五入」=最も近い浮動小数点数への丸め ¹⁰

正確には rounding to the nearest even となる。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...IEEE754-1985 ¹¹

“Standard for Binary Floating-Point Arithmetic” である。 http://grouper.ieee.org/groups/754/ を見よ。また大石先生の著作にも色々書いてある。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...Profil ¹²

PROFIL = Programmer's Runtime Optimized Fast Interval Library, BIAS = Basic Interval Arithmetic Subroutines.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... を利用した経験 ¹³

桂田研 2000 年度修士論文, 石川邦臣 http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/ishikawa-master.pdf, 鈴木康大 http://nalab.mind.meiji.ac.jp/~mk/labo/report/pdf/suzuki-master.pdf

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... そのビットを適当に設定することで浮動小数点演算の丸めモードを指定できる ¹⁴

具体的にどうするかを知りたければ、後述する BIAS のソースを読むと良い。

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... even ¹⁵

最も近い浮動小数点数 (それが二つある場合には、最下位ビットが 0 の方 -- 偶数 -- を採用) への丸め

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.