4.2 定義と Stetter の行列表現

前節に解説したタイプの公式のうち、$k=1$ の場合、 すなわち $1$ 段法を Runge-Kutta 型公式という。 いくつかの $(t,x)$ について、右辺の $f(t,x)$ を計算し、 それらの重みつき平均によって、適当な次数の (=その次数までの 真の解の Taylor 展開と一致するような)公式を作っている。 具体的には Runge-Kutta 型公式の一般形は

$$\left\{ \begin{array}{lll} x_{j+1}&=x_j+h\dsp\sum_{i=1}^s \mu_i... ...=1}^s\beta_{i \ell}k_\ell\right) & \hbox{($i=1,\cdots,s$)} \end{array}\right.$$

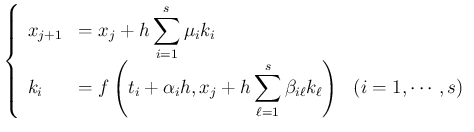
の形に書くことが出来る。ここで $s$ を段数 (number of stages) と呼ぶ。段数とは、要するに $1$ ステップ先に進めるために必要な $f$ の計算回数である⁶。

上の式は、 $k_1$ , $k_2$ , $\cdots$ , $k_s$ についての $s$ 元連立1次方程式を解いて、 その重みつき平均を $x_j$ に足して $x_{j+1}$ を求める、 という手順で使うことになる。

段数 $s$ と係数 $\{\alpha_i; 1\le i\le s\}$ , $\{\beta_{i j}; 1\le i, j\le s\}$ , $\{\mu_i; 1\le i\le s\}$ を選ぶとスキームが定まることになる。 それら係数を並べた

$$\begin{array}{c} \alpha_1\\ \alpha_2\\ \vdots \\ \alp... ...{2 s}\\ \vdots \\ \beta_{s s}\\ \mu_s \end{array}\right.$$

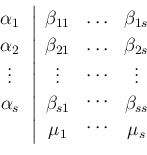
のような表を Stetter の行列表現 (Stetter's notation) と 呼ぶ⁷。

公式が前進型 (陽的、explicit)であるとは

$$i\le j\quad\Then\quad \beta_{i j}=0$$

が成り立つことを言う⁸。 このとき、$k_1$ , $k_2$ , $\cdots$ , $k_s$ の順に容易に計算できる。

公式が前進型でない場合、 公式が陰的 (implicit) であるという。 陰的な場合でも

$$i<j\quad\Then\quad \beta_{i j}=0$$

が成り立つ⁹場合は 半陰的 (semi-implicit) であるという。