Next: 3.1.2 これからの目標 Up: 3.1 はじめに Previous: 3.1 はじめに
常微分方程式というのは大雑把に言うと、「一つの実独
立変数 ![]() の未知関数
の未知関数 ![]() を求めるための問題で、
を求めるための問題で、![]() とその導関数
とその導関数
![]() ,
,
![]() ,
, ![]() ,
,
![]() についての方程式になっているもの」のことです。
(以下では
についての方程式になっているもの」のことです。
(以下では
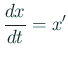 ,
,
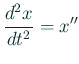 ,
,
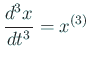 ,
, ![]() のような書き方もします。)
のような書き方もします。)
ここに例としてあげた方程式はいずれも割とポピュラーなものなのですが、
見覚えがあるでしょうか?どの場合もこれらの方程式だけでは解が一つに定ま
らず、何らかの条件を付け足すことによって初めて解が決定されます。その条
件として、ある特定の ![]() の値
の値 ![]() に対する
に対する ![]() の値
の値 ![]() や導関
数の値を指定するというタイプのものがよくありますが、そういうものを
初期条件と呼びます(これは
や導関
数の値を指定するというタイプのものがよくありますが、そういうものを
初期条件と呼びます(これは ![]() が時刻を表す変数で、
が時刻を表す変数で、![]() を現象が
始まる時刻のように解釈するからでしょう)。
を現象が
始まる時刻のように解釈するからでしょう)。
例えば、上の例 1, 3 に対して