Next: この文書について... Up: FreeFem++ の紹介 Previous: FreeFem++ のマニュアル3.9 から: Stokes方程式の
内部で熱が発生する (or 熱が吸収される) 場合の熱方程式の初期値境界値問題
を考える。
変数 ![]() については(後退)差分近似する。すなわち
については(後退)差分近似する。すなわち
![]() ,
,
![]() とおいて、
とおいて、
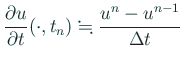
弱形式は
![$\displaystyle \left(\frac{u^{n}-u^{n-1}}{\Delta t},v\right)
+\langle u^{n},v\rangle-(f,v)-[g_2,v]=0.
$](img125.gif)
既に ![]() が “分かっている” とき、
これは
が “分かっている” とき、
これは ![]() についての Poisson 方程式もどきに対する弱形式であり、
これまでとほぼ同様にして解くことが出来る。
についての Poisson 方程式もどきに対する弱形式であり、
これまでとほぼ同様にして解くことが出来る。
| heatB.edp |
|---|
// heatB.edp
// http://nalab.mind.meiji.ac.jp/~mk/program/fem/heatB.edp
// 菊地文雄, 有限要素法概説, サイエンス社のPoisson方程式の問題の非定常版
// 時刻については後退Euler法 (陰解法)
int i,m=10;
real Tmax=10, tau=0.01, t;
// コメント・アウトすると、m, tau, theta が実行時に変更できるようになる
// cout << "m dt theta: ";
// cin >> m >> tau >> theta;
// cout << "m=" << m << ", tau=" << tau << ", theta=" << theta << endl;
mesh Th=square(m,m);
plot(Th,wait=true);
fespace Vh(Th,P1);
func f=1;
func g1=0;
func g2=0;
func u0=sin(pi*x)*sin(pi*y);
Vh u=u0,uold,v;
plot(u,cmm="t=0",wait=1);
problem heat(u,v,init=i)=
int2d(Th)(u*v+tau*(dx(u)*dx(v)+dy(u)*dy(v)))
-int2d(Th)(tau*f*v)
-int1d(Th,2,3)(tau*g2*v)
-int2d(Th)(uold*v)
+on(1,4,u=g1);
for (i=0;i<Tmax/tau;i++) {
uold=u;
t=(i+1)*tau;
heat;
plot(u,cmm="t="+t,wait=0); // ps="heat"+i+".ps" として保存することも可能
}
plot(u,wait=1);
|
ループの制御変数を i という変数にして、
problem に ,init=i と書き足すのがミソ。
最初は i が 0 であるので、init が False であるが、
それ以降は
![]() であるので、init が True である、
つまり LU 分解済みだ、と指示するわけである。
であるので、init が True である、
つまり LU 分解済みだ、と指示するわけである。
時間が経過すると、 定常解に収束する(Poisson方程式の解に近く)様子が見える。