Next: 4 行列が疎でも逆行列が疎とは限らない Up: MATLAB 使い方入門 Previous: 2 コマンド等覚え書き
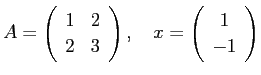
に対して、
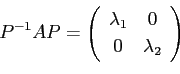 となる
となる
| MATLAB のコマンド・メモ (1) | ||||||||||||||||
|
>> a=[1,2;2,3]
a =
1 2
2 3
>> x=[1;-1]
x =
1
-1
>> b=a*x
b =
-1
-1
>> a\b
ans =
1.0000
-1.0000
>> inv(a)
ans =
-3.0000 2.0000
2.0000 -1.0000
>> inv(a)*a
ans =
1 0
0 1
>> eig(a)
ans =
-0.2361
4.2361
>> [p lambda]=eig(a)
p =
-0.8507 0.5257
0.5257 0.8507
lambda =
-0.2361 0
0 4.2361
>> inv(p)*a*p
ans =
-0.2361 -0.0000
-0.0000 4.2361
>>
最後の ![]() の計算は、丸め誤差の影響で、完全な対角行列にはなっ
ていない (が、誤差は
の計算は、丸め誤差の影響で、完全な対角行列にはなっ
ていない (が、誤差は ![]() のオーダーで十分小さい)。
のオーダーで十分小さい)。
桂田 祐史