D..4 Gauss の消去法

Gauss の消去法というのは、 要するに中学校で習った (未知数を一つ一つ消去して減らしていく) 消去法である。

例として次の方程式を取りあげて説明しよう。

$$\left\{ \begin{array}{rcrcrl} 2x_1&+&3x_2&-&x_3&=5 4x_1&+&4x_2&-&3x_3&=3 -2x_1&+&3x_2&-&x_3&=1. \end{array} \right.$$ (3)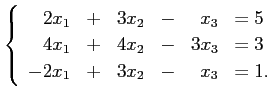

線形代数で習う掃き出し法では、 係数行列と右辺のベクトルを並べた行列を作り、それに

(1)

ある行に 0 でない定数をかける。

(2)

二つの行を入れ換える。

(3)

ある行に別の行を加える。

のような操作 -- 行に関する基本変形と呼ぶ -- をほどこして、 連立方程式の係数行列に相当する部分を単位行列にするのであった。

$$\left( \begin{array}{cccc} 2&3&-1&5 \\ 4&4&-3&3 \\ -2&3&-1&... ...}{2}&\frac{5}{2} \\ 0&-2&-1&-7 \\ 0&6&-2&6 \end{array} \right)\rightarrow$$

$$\rightarrow \left( \begin{array}{cccc} 1&\frac{3}{2}&-\frac{1}... ...\\ 0&1&\frac{1}{2}&\frac{7}{2} \\ 0&0&1&3 \end{array} \right) \rightarrow$$

$$\rightarrow \left( \begin{array}{cccc} 1&0&0&1 \\ 0&1&0&2 \\... ...array} \right) =\left( \begin{array}{c} 1\\ 2\\ 3 \end{array} \right).$$

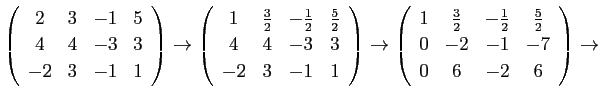
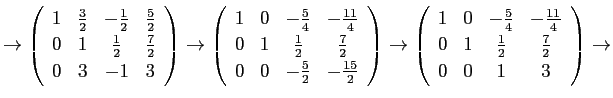
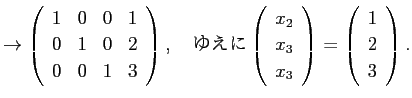
ガウスの消去法も、前半の段階はこの方法に似ていて、同様の変形を用いて 掃き出しを行なうのだが、以下のように対角線の下側だけを 0 にする。

$$\left( \begin{array}{cccc} 2&3&-1&5 \\ 4&4&-3&3 \\ -2&3&-1&... ...n{array}{cccc} 2&3&-1&5 \\ 0&-2&-1&-7 \\ 0&0&-5&-15 \end{array} \right).$$

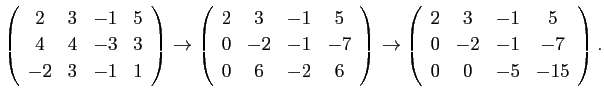
最後の行列は

$$2x_1+3x_2-x_3=5, \quad -2x_2-x_3=-7, \quad -5x_3=-15$$

ということを表しているので、後の方から順に

$$x_3=\frac{-15}{-5}=3, \quad x_2=\frac{-7+x_3}{-2}=2, \quad x_1=\frac{5-3x_2+x_3}{2}=\frac{5-3\times 2+3}{2}=1$$

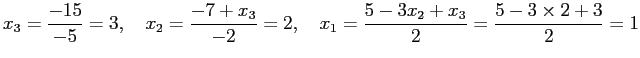
と解くことが出来る。前半の対角線の下側を 0 にする掃き出しの操作を 前進消去 (forward elimination)、後半の代入により解の値を求める 操作を後退代入 (backward substitution) と呼ぶ。