9.2 行列の等比級数

今度は正方行列 $A$ (ただし $A$ のスペクトル半径 は $1$ より小さいとする) の等比級数

$$I+A+A^2+A^3+\cdots =\sum_{n=0}^\infty A^n$$   $$\mbox{($I$ は単位行列)}$$

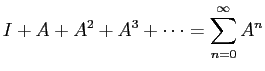
を考える。この級数は解析学では Neumann 級数と呼ばれる。

以下の実験は前節の続きで行うことを想定している。 Octave を終了してしまっている場合は、

この節の実験に先立ち必要なこと

n=5
a=rand(n,n)
r=max(abs(eig(a)))
a=a/r
a=0.9*a

を実行しておこう。

Neumann 級数の部分和

$$S_n=\sum_{k=0}^n A^k$$

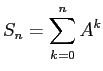
を計算する Octave プログラム neuamnn.m を用意した。

neumann.m

   1 % neumann.m --- 行列の Neumann 級数 (等比級数) の第 N 部分和
   2 function s = neumann(a,N)
   3   [m,n] = size(a);
   4   if m ~= n
   5     disp('aが正方行列でない！');
   6     return
   7   end
   8   % 第 0 項  S_0 = I
   9   s = eye(n,n);
  10   % 第 1 項  S_1 = I + a
  11   t = a; s = s + t;
  12   % 第 2〜N 項まで加える (t が a^n になるようにしてある)
  13   for k=2:N
  14     t = t * a;
  15     s = s + t;
  16   end

これを ~re00018/neumann.m から、 Octave を実行するディレクトリィにコピーしよう。

こうしてコピーする

isc-xas05% cp ~re00018/neumann.m .

octave:17> c=eye(n,n)-a
octave:18> b=neumann(a,100)
octave:19> b*c
octave:20> b=neumann(a,1000)	← もう少し精度を上げてみる
octave:21> b*c
octave:22> format long	← お望みなら表示桁数を上げて
octave:23> b*c

Neumann 級数の (部分) 和 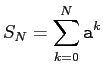$S_N=\dsp\sum_{k=0}^N \texttt{a}^k$ に $C=I-\texttt{a}$ をかけた結果が単位行列に非常に近いことが分かる。 種明かしをすると、

$$\sum_{n=0}^\infty A^n = (I-A)^{-1}$$

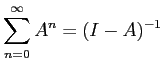
が成り立つ。これは等比級数の和の公式

$$\sum_{n=0}^\infty r^n=\frac{1}{1-r}$$   $$\mbox{(ただし $r$ は $\vert r\vert<1$ を満たす複素数)}$$

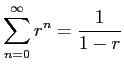
の一般化である。