A..1 nv_to_dim2.m

2次元長方形領域における、 Neumann 境界条件あるいは free edge の境界条件を課した境界値問題の 差分法プログラムでは、 $U_{ij}$ を $u(x_i,y_j)$ の近似として、

$$\sharp \Vector{V}= \begin{array}{ccccc} \biggl(\frac{U_{00}}{2},&\frac{U... ...cdots, &\frac{U_{N_x-1,N_y}}{\sqrt{2}},&\frac{U_{N_xN_y}}{2}\biggr) \end{array}$$

で定まるベクトル $\Vector{V}$ (順番に1次元的に並べてある) を用いて、差分方程式を行列表現している。 $\Vector{V}$ が v という1次元配列に記憶されているとき、

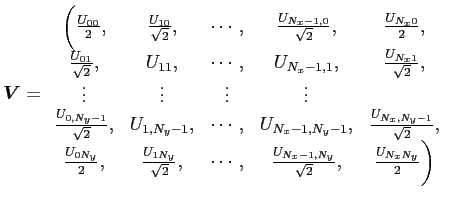 vvv=zeros(nx+1,ny+1);
 vvv(:)=v;

とすることで、2次元配列 vvv に変換できる。

$$= \left( \begin{array}{ccccc} \frac{U_{00}}{2},&\frac{U_{10}}{\sq... ...ots, &\frac{U_{N_x-1,N_y}}{\sqrt{2}},&\frac{U_{N_xN_y}}{2} \end{array} \right).$$

ここで MATLAB の2次元配列が、 FORTRAN のそれと同じ順番で (メモリー中に) 並んでいることを使っている。

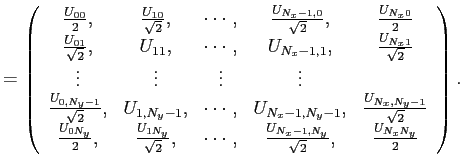確認

>> x=1:30;
>> y=zeros(6,5);
>> y(:)=x

y =

     1     7    13    19    25
     2     8    14    20    26
     3     9    15    21    27
     4    10    16    22    28
     5    11    17    23    29
     6    12    18    24    30

後は一番上の行、一番下の行、一番左の列、一番右の列に $\sqrt{2}$ を かければ

$$\left( \begin{array}{ccccc} U_{00},&U_{10},&\cdots,&U_{N_x-1,0}... ... U_{0N_y},&U_{1N_y},&\cdots, &U_{N_x-1,N_y},&U_{N_xN_y} \end{array}\right).$$

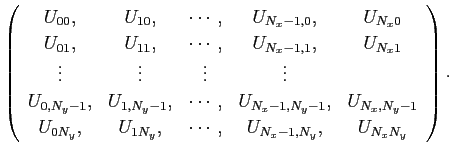
ところが、contour() や mesh() などの描画用の関数は、 Z(j,i)$=u_{ij}$ のように 「添字が j,i の順番に並べてある」ことを想定している (なぜだろう？)。理由はともあれ、そうするには単に転置をすれば良い。

(最初に $\Vector{V}$ の定義で添字を逆にしておけば、 転置なんてことをしなくて済むわけだけど、 いまさら書き換えるのは面倒なので、 転置の手間には目をつむることにする。)

% nv_to_dim2.m
%   Naummann境界条件の問題の差分解を2次元配列に変換
%   written by Masashi Katsurada
%   modified by Masashi Katsurada on 2012/9/29
%
% example:
%   [v,d]=eigs(plate_f1(N,0.3),200,0);
%   u=nv_to_dim2(v(:,201-n),N,N);
%   x=0:1/N:1; y=0:1/N:1;
%   u=u';
%   mesh(x,y,u);
%   contour(x,y,u);

function u=nv_to_dim2(v,nx,ny)
  u=zeros(nx+1,ny+1);
  u(:)=v;
  u(1,:)=u(1,:)*sqrt(2);
  u(nx+1,:)=u(nx+1,:)*sqrt(2);
  u(:,1)=u(:,1)*sqrt(2);
  u(:,ny+1)=u(:,ny+1)*sqrt(2);