

Next: 2 the shortest introduction
Up: How to use Hirano's
Previous: How to use Hirano's
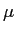 : given positive constant (Poisson ratio of the material),
: given positive constant (Poisson ratio of the material),
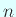 : the outward unit normal vector of the boundary,
: the outward unit normal vector of the boundary,
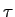 : the unit tangential vector of the boundary.
: the unit tangential vector of the boundary.


Next: 2 the shortest introduction
Up: How to use Hirano's
Previous: How to use Hirano's
桂田 祐史
2014-05-27
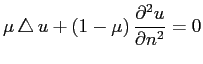 (on
(on 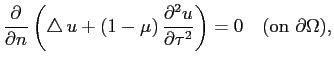
![]() : given positive constant (Poisson ratio of the material),
: given positive constant (Poisson ratio of the material),
![]() : the outward unit normal vector of the boundary,
: the outward unit normal vector of the boundary,
![]() : the unit tangential vector of the boundary.
: the unit tangential vector of the boundary.