C. 周期を数値積分で求める

ははみまかりける年某月某日、学生Yの襲撃に会う。 何でも振り子の周期を求めるために、 端点に特異性のある定積分を計算するように指示されたけど、 自分でネットを徘徊して、 変数変換によって特異性を除去してから台形則で計算したら (おおっ)、 粗い分割で非常な高精度を達成できた、という。 実質的に第2種完全楕円積分

$$K(k)=\int_{0}^{\pi/2}\frac{\D t}{\sqrt{1-k^2 \sin^2 t}}$$

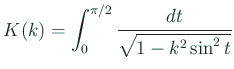
の計算に帰着させたらしい。

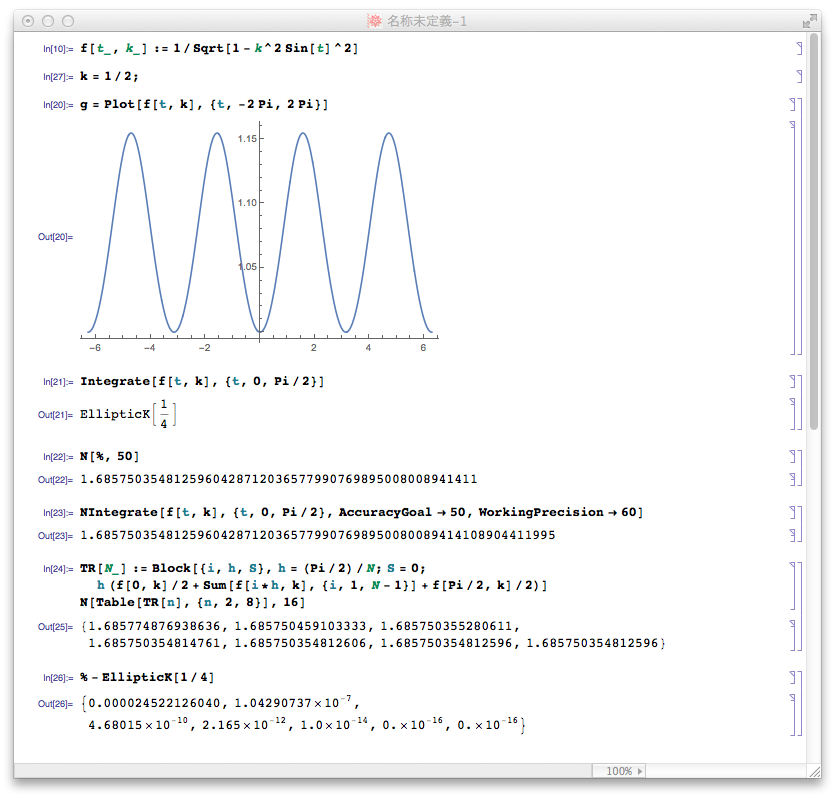
台形則で高精度…あれだな、きっと。ちょっとやってみよう。 まずは Mathematica で。

$k=1/2$ のときの $K(k)$ の値

f[t_,k_]:=1/Sqrt[1-k^2 Sin[t]^2]
k=1/2
g=Plot[f[t,k],{t,-Pi,Pi}]

被積分関数の周期は $\pi$ か。

Integrate[f[t,k],{t,0,Pi/2}]

→ EllipticK[1/4] と表示されるけれど、 これは Mathematica 方言で、本当は $K(1/2)$ ということだな。

N[%,50]

→ 1.6857503548125960428712036577990769895008008941411 となる。
ちなみに Mathematica で数値積分をするのは、NIntegrate[] だ。

NIntegrate[f[t, k], {t, 0, Pi/2}, AccuracyGoal -> 50, WorkingPrecision -> 60]

さて、それで台形則をしてみる。

TR[N_] := Block[{i, h, S}, h = (Pi/2)/N; S = 0; 
  h (f[0, k]/2 + Sum[f[i*h, k], {i, 1, N - 1}] + f[Pi/2, k]/2)]
N[Table[TR[n], {n, 2, 8}], 16]
%-EllipticK[k^2]

{0.000024522126040, 1.04290737*10^-7, 4.68015*10^-10, 2.165*10^-12, 
 1.0*10^-14, 0.*10^-16, 0.*10^-16}

なるほど、これは凄い。

実質的に、有名な

「解析的周期関数の1周期区間の積分は、 台形則で非常に高精度に計算できる」

という数値積分の常識の実例に遭遇したわけだ。

Cのプログラムを示せば、

period.c

#include <stdio.h>
#include <math.h>

double k = 0.5;

double sqr(double x) { return x * x; }

double f(double x)
{
  return 1 / sqrt(1- sqr(k * sin(x)));
}

int main(void)
{
  int i, n;
  double h,s,pi;

  pi = 4 * atan(1.0);
  for (n = 2; n <= 8; n++) {
    h = pi / 2 / n;
    s = (f(0) + f(pi/2)) / 2;
    for (i = 1; i < n; i++)
      s += f(i*h);
    s *= h;
    printf("%2d %20.15f\n", n, s);
  }
}

$ gcc period.c
$ ./a.out
 2    1.685774876938636
 3    1.685750459103333
 4    1.685750355280611
 5    1.685750354814761
 6    1.685750354812606
 7    1.685750354812596
 8    1.685750354812596
$

ふむふむ (区間を7等分で倍精度一杯の精度だ)。 AGM とどっちが速いんだろう。

それにしても、自力でそういう工夫をして、 高精度な結果が得られたことを不思議に思って追求して質問に来るとは、 大したものだと思う。