Next: 3 (Bochner 積分版) 微分積分学の基本定理 Up: Banach 空間における微積分の基本定理 Previous: 1 (普通の微積分版) 微分積分学の基本定理
この節の内容は Lebesgue 積分の常識で、 多くのテキストに載っているが、 関連する結果が非常に豊富という点で 特に吉田 [3] を強く推奨しておく。
この節の内容を一言でまとめると、 『絶対連続であれば、 ほとんど到るところ微分できて、 「自然な」公式が成り立つ』となる。 こういう言葉はないが、 「ルベーグの意味で微分可能」 とでも言うにふさわしい性質である。
![\begin{jtheorem}[Lebesgue の微分定理 --- 微積分の基本定理$\mathrm{I...
...laymath}
y'(t)=x(t)\quad\mbox{a.e. on $[a,b]$}.
\end{displaymath}\end{jtheorem}](img17.gif)
|
ある意味で逆が成立する。
![\begin{jtheorem}[Radon-Nikodym の定理]
絶対連続ならば可積分関数�...
...splaymath}
y'(t)=x(t)\quad\mbox{($t\in[a,b]$)}.
\end{displaymath}\end{jtheorem}](img18.gif)
|
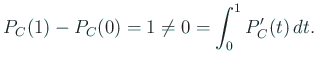
![\begin{jtheorem}[微積分の基本定理$\mathrm{II}'$]
$y\in\mathrm{AC}([a,b]...
...��で存在を保証されるところの微分係数である。
\end{jtheorem}](img25.gif)
|
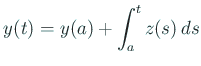
これから、ほとんどすべての
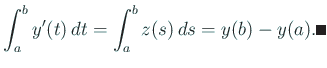
![\begin{jtheorem}[微積分の基本定理$\mathrm{III}'$\ (部分積分)]
$x$, ...
...��で存在を保証されるところの微分係数である。
\end{jtheorem}](img33.gif)
|
が成り立つ (証明は普通の微積分の積の微分法)。 右辺の各項は可積分関数と連続関数の積であるから可積分であり、 それゆえ左辺も可積分である。積分すると
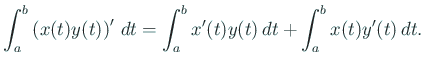
桂田 祐史