Next: 2.5 Legendreの関係式 Up: 2 楕円積分 Previous: 2.3 完全楕円積分の微分
(以下は本当かな?????)
![]() を変数とする限り、実関数の範囲では
を変数とする限り、実関数の範囲では
![]() とするのは自然
であり、そうすると
とするのは自然
であり、そうすると ![]() の範囲は
の範囲は
![]() とな
るが、
とな
るが、![]() を変数とした
を変数とした
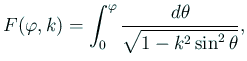 | ||
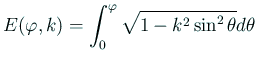 |
そうして拡張した場合も、
![]() ,
,
![]() は奇関数である。
そして、
は奇関数である。
そして、
![]() の場合に、
の場合に、
![]() と
と
![]() の
の
![]() の範囲のグラフを描いておく
(青色の線が
の範囲のグラフを描いておく
(青色の線が ![]() , 橙色の線が
, 橙色の線が ![]() )。
)。
![]() の外に出ても滑らかな曲線であることが分かる。
の外に出ても滑らかな曲線であることが分かる。
![\includegraphics[width=0.9\textwidth]{graph/FE01.eps}](img166.gif)
|
![\includegraphics[width=0.9\textwidth]{graph/FE05.eps}](img167.gif)
|
![\includegraphics[width=0.9\textwidth]{graph/FE09.eps}](img168.gif)
|