1 発端

それはK先生のところの学生I君からの相談で始まった。

数学概論応用編、 C¹第6章 p440 にある固有値問題

$$\frac{\partial ^4u}{\partial x^4} = \lambda u \quad\hbox{in $[0,1]$,}$$

$$u(0) = u'(0)=0,$$

$$u''(1) = u'''(1)=0$$

の数値計算がK先生から彼に与えられた課題。 本に書いてある計算法は次の通り。数列 $\{a_{ij}\}$ , $\{b_{ij}\}$ を

$$a_{ij} = \frac{i(i+1)j(j+1)}{i+j-1}, \quad b_{ij} = \frac{1}{i+j+3},$$

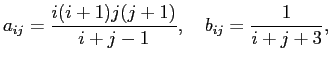
で定めて、各 $N=1,2,\cdots$ に対して $N$ 次正方行列 $A=A^{(N)}$ , $B=B^{(N)}$ を

$$A=(a_{ij}), \quad B=(b_{ij})$$

で定めた時の一般化固有値問題

$$\det(A-\lambda B)=0$$

の解を小さい順に並べたものを $\lambda^{(N)}_1, \lambda^{(N)}_2,\cdots, \lambda^{(N)}_N$ とする。これから

$$\lambda_i = \lim_{N\to+\infty}\lambda^{(N)}_i \quad\hbox{($i\in{\bf N}$)}$$

によって得られる $\{\lambda_i; i\in{\bf N}\}$ が最初の固有値問題の解になる。

行列の次数を $N$ として、 $N$ が小さい時の $\lambda^{(N)}_i$ の計算値は載っている。まず $N=1$ の時、

$$\lambda^{(1)}_1=20,$$

$N=2$ の時

$$\lambda^{(2)}_1=12.480, \quad \lambda^{(2)}_2=1211.520$$

となるそうだ。

一般化固有値問題というと、どういう問題であるか聞いたことはあるものの、 具体的にどうやって解くのがカシコイというような知識はほとんどなかった。 典型的な``教えながら勉強する''パターンになりそうだ、と思った。