Next: 4.2 ベクトルの扱いの練習 Up: 4 練習問題 Previous: 4 練習問題
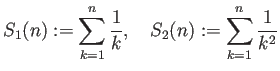
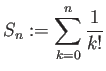 を計算して結果を表示するプログラムを
書け (
を計算して結果を表示するプログラムを
書け (
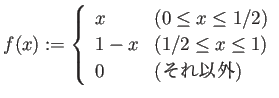
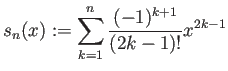
x = r * sin(theta) * cos(phi); y = r * sin(theta) * sin(phi); z = r * cos(theta); |
d2p(x, y, z, &r, &theta, &phi); |
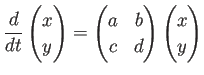 ,
,
(
![]() は狭義単調減少で、
は狭義単調減少で、
![]() ,
,
![]() であるから、
区間
であるから、
区間 ![]() にただ1つの実数解を持つことが分かる。)
にただ1つの実数解を持つことが分かる。)
桂田 祐史