Next: 3.8 while による繰り返しと if Up: 3 簡単な数値計算プログラミングで良く使う機能 Previous: 3.6 for 文による繰り返し
級数の和
|
|
|
次のプログラムは、与えられた自然数 ![]() に対して
に対して
![]() を計算して表示するものである。
を計算して表示するものである。
| prog07.c |
/*
* prog07.c --- for 文による繰り返し (2)
*/
#include <stdio.h>
int main(void)
{
int i, n;
double s;
printf("自然数を一つ入力してください: ");
scanf("%d", &n);
s = 0.0;
for (i = 1; i <= n; i++) {
/* 次の文では s に i を加えている。これは s = s + i * i; とも書ける。 */
s += i * i;
}
printf(" 1 から %d までの自然数の平方の和=%g\n", n, s);
return 0;
}
|
後の練習問題にしておいた、
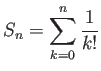 を計算するプログラムを自力で
書いてみると良い。
ヒント:
一般項
を計算するプログラムを自力で
書いてみると良い。
ヒント:
一般項 ![]() も漸化式で計算すると都合が良い。
「漸化式を使って計算しよう」 という
資料を準備しておいた。
も漸化式で計算すると都合が良い。
「漸化式を使って計算しよう」 という
資料を準備しておいた。