Next: 6.2 DE公式の誤差解析 Up: 6 複素関数論を用いたもう一つの誤差解析 Previous: 6 複素関数論を用いたもう一つの誤差解析
実解析的な
![]() に対して、
に対して、
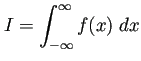 |
(39) |
![]() ,
,
![]() とするとき、
とするとき、
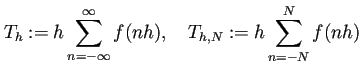 |
(40) |
![]() はある
はある ![]() に対して、
に対して、
| (41) |
実際の数値計算では、
![]() を有限和で置き換えた
を有限和で置き換えた ![]() を使わざるを得ない。
その場合は、関数
を使わざるを得ない。
その場合は、関数 ![]() の遠方での減衰の具合が問題となる。
の遠方での減衰の具合が問題となる。
そこで遠方での減衰の具合の物差しとなるような正則関数
![]() を固定して、
を固定して、
![]() 定数
定数![]() (
(
![]() ) を満たす
) を満たす ![]() について考える。
について考える。
![]() で正則で 0 にならない関数
で正則で 0 にならない関数 ![]() を一つ取り、
を一つ取り、
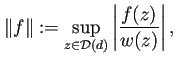 |
(42) | |
| (43) |
![]() は、
は、
![]() のときの
のときの ![]() の減衰の度合いを示す関数である。
の減衰の度合いを示す関数である。
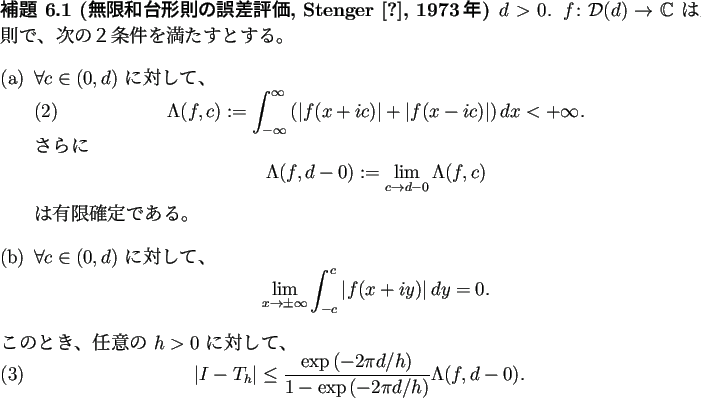
|
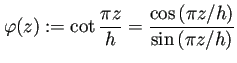 において、
において、
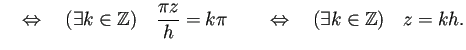
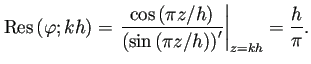
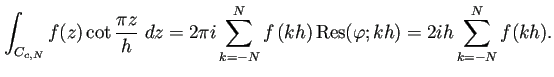
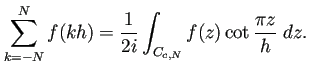
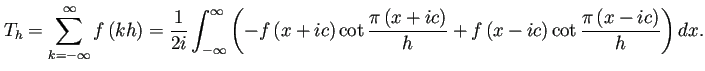
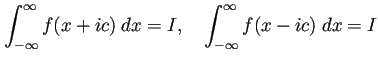
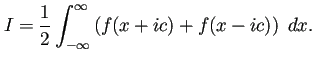
![$\displaystyle T_h-I=\int_{-\infty}^\infty
\left[
f(x+ic)\frac{\exp\frac{2\pi ...
...ac{\exp\frac{-2\pi i(x-ic)}{h}}
{1-\exp\frac{-2\pi i(x-ic)}{h}}
\right]
\Dx
$](img314.png)
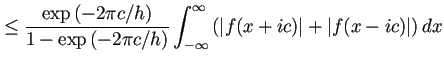 |
||
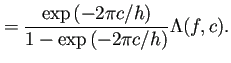 |
![]() の誤差については、次の定理を得る。
の誤差については、次の定理を得る。

|
桂田 祐史