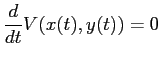

Next: 5.5 渡邉隆之『戦闘の数理』
Up: 5 2010年度卒研
Previous: 5.3 小釜燈台『グライダーの数理』
捕食者 (predator) と被食者 (prey) の関係にある2種の生物群の増減を
モデル化した、次の方程式を Lotka-Voltarra の方程式と呼ぶ。
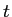 は時刻、
は時刻、
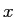 が被食者の個体数、
が被食者の個体数、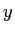 が捕食者の個体数である。
が捕食者の個体数である。
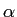 ,
, 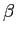 ,
, 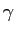 ,
, 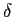 は正の定数である。
は正の定数である。
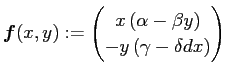 とおくとき、ヤコビ行列は
とおくとき、ヤコビ行列は
平衡点は
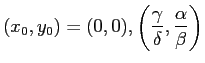 の2点である。
の2点である。
前者は実際にはほとんど無意味である (どちらの生物も存在しない)。
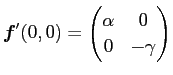 の固有値は
の固有値は 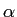 ,
, 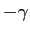 であるから、
であるから、
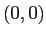 は鞍点である。
は鞍点である。
後者について、
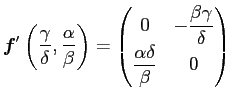 で、固有値は
で、固有値は
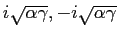 である。
である。
とおくとき、
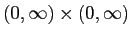 における解
における解
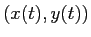 に対して、
に対して、
- Vito Volterra,
Variazioni e fluttuazioni del numero d'individui in specie conviventi,
Mem Acad Lincei Roma 2 (1926), pp. 31-113.
http://www.liberliber.it/biblioteca/v/volterra/variazioni_e_fluttuazioni/pdf/volterra_variazioni_e_fluttuazioni.pdf
数理解析研究所講究録 1448巻, 2005年, pp. 151-161 に解説がある。


Next: 5.5 渡邉隆之『戦闘の数理』
Up: 5 2010年度卒研
Previous: 5.3 小釜燈台『グライダーの数理』
桂田 祐史
2015-12-24
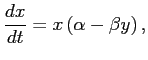
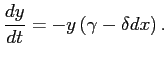
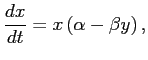
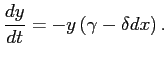
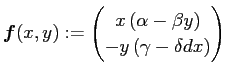 とおくとき、ヤコビ行列は
とおくとき、ヤコビ行列は
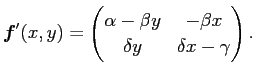
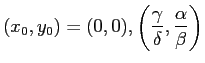 の2点である。
の2点である。
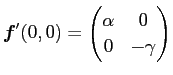 の固有値は
の固有値は ![]() ,
, ![]() であるから、
であるから、
![]() は鞍点である。
は鞍点である。
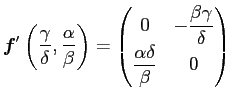 で、固有値は
で、固有値は
![]() である。
である。