Next: 7.2 空間曲線 Up: 7 パラメーター曲線を描く Previous: 7 パラメーター曲線を描く
![]() ,
, ![]() とパラメーター表示される平面曲線を描くには、
set parametric としてから、
plot f(t),g(t) とすればよい。
このモードから抜けるには set noparametric とする。
とパラメーター表示される平面曲線を描くには、
set parametric としてから、
plot f(t),g(t) とすればよい。
このモードから抜けるには set noparametric とする。
特に図形の「形」が気になる場合は、set size ratio -1 は必須かも。 例えば楕円
![$\displaystyle \left\{
\begin{array}{ll}
x = 3\cos t\\
y = 2\sin t
\end{array} \right.
\quad\mbox{($t\in[0,2\pi]$)}
$](img66.gif)
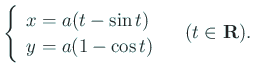
アルキメデス螺旋 ![]() を二つの方法で描いて比較してみよう。
を二つの方法で描いて比較してみよう。
# archimedes1.gp set parametric set samples 200 set xrange [-30:30] set yrange [-30:30] set size square plot [0:10*pi] t*cos(t),t*sin(t) pause -1 set term postscript eps color set output "archimedes1.eps" replot |
# archimedes2.gp set parametric set samples 200 set size ratio -1 plot [0:10*pi] t*cos(t),t*sin(t) pause -1 set term postscript eps color set output "archimedes2.eps" replot |
![\includegraphics[height=7cm]{archimedes/archimedes1.eps}](img71.gif)
|
![\includegraphics[height=7cm]{archimedes/archimedes2.eps}](img72.gif)
|
| 楕円 |
# parametric-1.gp --- 楕円 set parametric a=3 b=2 plot [0:2*pi] a*cos(t),b*sin(t) pause -1 set term postscript eps color set output "parametric-1.eps" replot |
| 双曲線 |
# parametric-2.gp --- 双曲線 set parametric set size ratio -1 a=3;b=2 plot [-2:2] a*cosh(t),b*sinh(t),-a*cosh(t),b*sinh(t) pause -1 set term postscript eps color set output "parametric-2.eps" replot |