Next: 14 cal コマンドの結果がおかしい … Up: 2025年のコンピューターノウハウ (Mac) Previous: 12 MacPorts での boost
このところやっている数値計算ネタで、Mac とは直接的な関係のない話。 数値計算ライブラリィ探し、ということだけど、 Mathematica とか Python には複素変数版がすでに入っているけれど、 C や C++ でプログラムを書くにはいいものが見つからなくて、とりあえず自作した、 というあらすじ。そのうち「こうすればいいんだ」という続報を書き足すかも。
関数論のうちであまりよく知らないところの復習をしていて、 学生の頃から気になっていた楕円積分と対峙することとなった。
その数値計算について、知っていてしかるべきだったのに、全く知らなかった、 ということがあったので、自分の整理のためにも簡単にメモしておく。
まず微積分の復習から。
2変数の有理関数 ![]() と多項式
と多項式 ![]() に対して、不定積分
に対して、不定積分
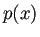 は、
は、![]() の次数が
の次数が![]() 以下だったら初等関数の範囲で
求めることができる(微積分ネタとなる)が、次数が3以上の場合は、
特殊な例外をのぞいて求まらない。
特に
以下だったら初等関数の範囲で
求めることができる(微積分ネタとなる)が、次数が3以上の場合は、
特殊な例外をのぞいて求まらない。
特に ![]() の次数が 3,4の場合は楕円積分と呼ぶ。
学生の頃の感想としては、
の次数が 3,4の場合は楕円積分と呼ぶ。
学生の頃の感想としては、
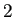 の段階で、結構面倒な計算をやらされて、
正直ちょっと嫌だけれど、その先があるのかぁ、大変だなあ。
の段階で、結構面倒な計算をやらされて、
正直ちょっと嫌だけれど、その先があるのかぁ、大変だなあ。
数学に少しはまりかけると、高木貞治「近世数学史談」とか読んで、 何か良く分からないけれど、すごそう、大変だったんだなあ、ということが知れる。 Legendre という数学者が楕円積分について記念碑的な著書を書いたけれど、 (楕円積分の逆関数である) 楕円関数の研究という大躍進はその後にやってきたとか。
授業でも、楕円関数や Riemann 面について教わる訳だけれど、 そういうのを何かに使うというのは経験がなかった。 時々、これは楕円積分、楕円関数を使って扱えるというのに遭遇した訳だけど、 勉強するコストを考えて後回しにしてきた面がある。
定積分の値が知りたいだけならば、数値積分という手がある。特異性があっても、 二重指数関数型数値積分公式とか使うとうまく計算できる、 というようなのは講義でも話したりする話題だ。 そういう立場からは、扱った例の中に楕円積分に分類されるものもありますね、 くらいのものだ。
今回は、与えられた領域の等角写像やその逆関数を計算する問題を考えていて、 「有名な」Schwarz-Christoffel 変換を初めてちゃんと学ぶこととなった。 カッコ付きなのは、取り上げていない関数論のテキストも結構あって、 取り上げていても証明略とか、説明がわかりにくいとかいうのが多かったので、 実は顔は知っているけれど、どんな人かはよく存じ上げません、 という感じ?
その勉強もどうやら一段落して (とても面白かった)、
最後にやはり上半平面
![]() から長方形領域への双正則関数を求めるという定番問題の解を数値計算してみよう、
となった。
問題の設定のしかたによっては
から長方形領域への双正則関数を求めるという定番問題の解を数値計算してみよう、
となった。
問題の設定のしかたによっては
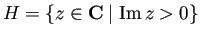
それを計算するためのライブラリィがあったはずだ。えーと、、、
Mathematica だと EllipticF[![]() ,m] というのがそれか。
これは
,m] というのがそれか。
これは
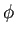
まずは論より run で、
F[z_,k_]:=EllipticF[ArcSin[z],k^2] |
ParametricPlot[ReIm[F[t,0.5]],{t,-10,10}]
|
あれ?![]() で左折して(上に向かって)ほしいのに右折している。
方向音痴だ。
まあこういうことは覚悟していた。
手短に原因を説明すると、ArcSin[
で左折して(上に向かって)ほしいのに右折している。
方向音痴だ。
まあこういうことは覚悟していた。
手短に原因を説明すると、ArcSin[![]() ]は、
]は、
![]() (
(![]() はいわゆる主値) と定義してあって、
はいわゆる主値) と定義してあって、
![]() と
と
![]() が分岐截線 (branch cut) だけれど、
右側の線上では下半平面と連続につながるようになっているから、である。
が分岐截線 (branch cut) だけれど、
右側の線上では下半平面と連続につながるようになっているから、である。
![]() は、私の頭の中では
は、私の頭の中では
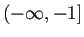 が第一近似で、
これは円弧三角形
が第一近似で、
これは円弧三角形
![]() の Schwarz-Christoffel 写像と解釈できるから、
上半平面に制限して連続になってくれることを期待するけれど
(Jordan領域の間の双正則関数は、閉包まで同相写像に拡張できるという、
Carathéodory の定理を思い出す)、
ライブラリィ関数としては、
の Schwarz-Christoffel 写像と解釈できるから、
上半平面に制限して連続になってくれることを期待するけれど
(Jordan領域の間の双正則関数は、閉包まで同相写像に拡張できるという、
Carathéodory の定理を思い出す)、
ライブラリィ関数としては、
![]() と定義してあるので、残念ながらそうはなっていないと。
まあ、奇関数にならないのも変な感じがするし、仕方がないのかな。
自作の myArcSin[] (上半平面に制限すると連続) で置き換えよう。
と定義してあるので、残念ながらそうはなっていないと。
まあ、奇関数にならないのも変な感じがするし、仕方がないのかな。
自作の myArcSin[] (上半平面に制限すると連続) で置き換えよう。
as[x_] := Which[x >= 1, Pi/2 + I Log[x + Sqrt[x^2 - 1]], True, ArcSin[x]]
myArcSin[z_] := If[Im[z] != 0, ArcSin[z], as[z]]
F2[z_, k_] := EllipticF[myArcSin[z], k^2]
gcurve2 = ParametricPlot[ReIm[F2[t, 0.5]], {t, -5, 5}]
|
これでどうなる?
うわあ。![]() では無事左折するようになったけれど、
今度は
では無事左折するようになったけれど、
今度は ![]() で右折してしまった…
これは
で右折してしまった…
これは ![]() のせいではなく、
EllipticF[] の値の選び方のせいである。
のせいではなく、
EllipticF[] の値の選び方のせいである。
こちらも分岐截線のところで、崖の下と上とどちらを選ぶかの話で、 ArcSin[] の方は崖の上の方を選ぶべきだったけれど、 今度は崖の下の方を選ぶべきと。
もうひと頑張り… まあ、なんとか出来ました。どうやったかは内緒 (ちょっとその場しのぎの技を使いました)。
今は便利なツールがあって、なぜ考えていたようにならないのか、 すぐ画面で見えるようになっているから、1日の間に解決したけれど、 そうでなければ大変だったろうと思う。
意外と使いにくいな EllipticF[]。
数学のテキストを見ると ![]() というのは良く出て来るけれど、
それをコンピューターで用意されている
というのは良く出て来るけれど、
それをコンピューターで用意されている
![]() (EllipticF[]) を使って計算するのは大変だ、
ということだ。
何か私の知らないうまい手があるのかしら?
(EllipticF[]) を使って計算するのは大変だ、
ということだ。
何か私の知らないうまい手があるのかしら?
それで見つけたのが、今回のお題の Carlson の対称楕円積分である。 たくさん種類があるけれど、代表的なのは
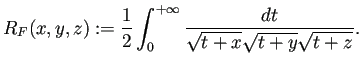
Legendre の関数 ![]() は、被積分関数の分母の零点が
は、被積分関数の分母の零点が ![]() ,
, ![]() で、
それを
で、
それを ![]() という1つのパラメーターで表したけれど、
という1つのパラメーターで表したけれど、
![]() は分母の零点をそのまま
(
は分母の零点をそのまま
(![]() はかけてあるか)
はかけてあるか) ![]() ,
, ![]() ,
, ![]() と与えている。
変数の数が増えたけれど、対称性がある。
と与えている。
変数の数が増えたけれど、対称性がある。
![]() の他にどういう関数が用意されているかは、Wolfram MathWorld の
の他にどういう関数が用意されているかは、Wolfram MathWorld の
https://mathworld.wolfram.com/CarlsonEllipticIntegrals.htmlが手取り早い。
ちなみに ![]() があれば
があれば
![]() は
は
Carlson の楕円積分は、登場したのはそんなに古くはないけれど、 新しくもない。1977年の論文が最初とされているが、 それ以前からの研究の延長上にあるので、文献リストは結構長い (以下は1963年からの論文と著書である -- [#!Carlson1963!#], [#!Carlson1964!#], [#!Carlson1977!#], [#!Carlson1977a!#], [#!Carlson1978!#], [#!Carlson1979!#], [#!Carlson-Notis1981!#], [#!Carlson1987!#], [#!Carlson1988!#], [#!Carlson-Gustafson1994!#], [#!Carlson1995!#], [#!Carlson2010!#])。
これらの論文は “読解中” である。 自分の問題にとにかく応用しよう、 という観点からは、 第三者による解説 Press-Teukolsky [#!Press-Teukolsky1990!#] を最初に読むのが分かりやすいと思われる。
実は Carlson の対称楕円積分は、知っている人には常識的なことらしい。
Mathematica にも Python にもそれを計算するための関数が用意されている
(![]() は、Mathematica の場合 CarlsonRF[],
Python の場合 scipy.special.elliprf())。
は、Mathematica の場合 CarlsonRF[],
Python の場合 scipy.special.elliprf())。
以下は、 特殊関数についての有名な文献である Abramowitz-Stegun [#!Abramowitz-Stegun!#] の “現代化” といわれている NIST Handbook の§19.32 Conformal Map onto a Rectangle に載っていることである。
![]() とするとき、
とするとき、
x1 = 3; x2 = 2; x3 = 1;
f[z_] := CarlsonRF[z - x1, z - x2, z - x3]
ParametricPlot[ReIm[f[t]],{t,-10,10},PlotPoints->500]
|
あっけないくらい簡単ですね。まあ変数が ![]() である分、
である分、
![]() に近いから、ということはできるか。
に近いから、ということはできるか。
さて、私は古い人間なので、CやC++でガリガリとプログラムを書きたい。 それ以外にも、一体どうやって計算するのかに興味がある。 どこかにプログラムないかな… Boost にあるけれど、実変数専用だ (またかいな)。
仕方がないので、自分でなんとかしよう。 Legendre の楕円積分や Jacobiの楕円関数は、計算の仕方も非常に面白いけれど、 Carlson の楕円積分の計算も大変面白い。
上で紹介したPress-Teukolsky [#!Press-Teukolsky1990!#]に、 単精度実数版のFortran コードが載っているけれど、非常にコンパクトである。 そしてそれはほぼそのまま複素数版に書き換えることができる。
次は (内容は全く保証しないけれど)、C言語で ![]() を計算する関数である。
を計算する関数である。
| cdrf.c |
/*
* cdrf.c --- Carlson の対称楕円積分 RF を計算する関数 (しばらく工事中)
* William H. Press and Saul A. Teukolsky,
* Elliptic integrals, Computers in Physics, Vol. 4, pp. 92--96 (1990).
* ここに単精度実数版の Fortran プログラムが載っている。そのマイナーチェンジ。
*/
#include <stdio.h>
#include <stdlib.h>
#include <complex.h>
static double max(double a, double b, double c)
{
double t = a;
if (b > t)
t = b;
if (c > t)
t = c;
return t;
}
double complex cdrf(double complex x,
double complex y,
double complex z)
{
double ERRTOL = 0.0025, TINY = 1e-306, BIG = 1e306, THIRD = 1.0 / 3.0;
double C1 = 1.0 / 24.0, C2 = 1.0 / 10.0, C3 = 3.0 / 44.0, C4 = 1.0 / 14.0;
double complex alamb,ave,delx,dely,delz,e2,e3,sqrtx,sqrty,sqrtz, xt, yt, zt;
int count;
/* ERRTOL を 0.0025 にするのは Press-Teukolsky の論文に書いてあった。
TINY, BIG は IEEE 倍精度なのでテキトーに (あまり深く考えていない)。
実はそのチェックのコードは削除してしまった。
Computes Carlson's elliptic integral of the first kind, RF(x, y, z). x, y
and z must be non-negative, and at most one can be zero. TINY must be at
least 5 times the machine underflow limit, BIG at most one fifth the
machine overflow limit.
ここで non-negative と書いてあるが、実数版の制限で、複素数版には該当しない。
*/
if ((x==0.0 && y==0.0) || (y == 0.0 && z == 0.0) || (z==0.0 && x==0)) {
fprintf(stderr, "");
exit(-1);
}
xt=x;
yt=y;
zt=z;
count = 0;
do {
sqrtx=csqrt(xt);
sqrty=csqrt(yt);
sqrtz=csqrt(zt);
alamb=sqrtx*(sqrty+sqrtz)+sqrty*sqrtz;
xt=0.25*(xt+alamb);
yt=0.25*(yt+alamb);
zt=0.25*(zt+alamb);
ave=THIRD*(xt+yt+zt);
delx=(ave-xt)/ave;
dely=(ave-yt)/ave;
delz=(ave-zt)/ave;
count++;
}
while (max(cabs(delx),cabs(dely),cabs(delz)) > ERRTOL);
printf("count=%d\n", count);
e2=delx*dely-delz*delz;
e3=delx*dely*delz;
return (1.0+(C1*e2-C2-C3*e3)*e2+C4*e3)/csqrt(ave);
}
|
短くてシンプルなアリゴリズム。とても美しい (要点は[#!Press-Teukolsky1990!#]に書いてある)。
Carlson [#!Carlson1995!#] の、 第3節 Numerical checks の節にある数値例を試すプログラムをつけておく。
| cdrf.c |
/*
* testcdrf.c
* gcc -O -o testcdrf testcdrf.c cdrf.c
* Numerical Checks (Carlson 1995)
* RF(1,2,0) 1.3110287771460599052
* RF(i,-i,0) 1.8540746773013719184
* RF(i-1,i,0) 0.7961258658423391329 - 1.2138566698364959864 I
* RF(2,3,4) 0.58408284167715170669
* RF(i,-i,2) 1.04414456540643609311
* RF(i-1,i,1-i) 0.93912050218619371197 - 0.53296252018635269265 I
* RF(x,y,z) x,y,zに2つ以上0があってはいけない。
*/
#include <stdio.h>
#include <complex.h>
#include <math.h>
double complex cdrf(double complex, double complex, double complex);
int main(void)
{
double complex result, exact;
double error;
printf("I=%g+%gi\n", creal(I), cimag(I)); // complex.h で I が定義されている
exact = 1.3110287771460599052;
result = cdrf(1.0, 2.0, 0.0); error = cabs(exact - result);
printf("RF(1,2,0)=%.15f+%.15f i, 誤差=%e\n",
creal(result), cimag(result), error);
exact = 1.8540746773013719184;
result = cdrf(I, -I, 0.0); error = cabs(exact - result);
printf("RF(i,-i,0)=%.15f+%.15f i, 誤差=%e\n",
creal(result), cimag(result), error);
exact = 0.7961258658423391329 - 1.2138566698364959864i;
result = cdrf(I - 1.0, I, 0.0); error = cabs(exact - result);
printf("RF(i-1,i,0)=%.15f+%.15f i, 誤差=%e\n",
creal(result), cimag(result), error);
exact = 0.58408284167715170669;
result = cdrf(2.0, 3.0, 4.0); error = cabs(exact - result);
printf("RF(2,3,4)=%.15f+%.15f i, 誤差=%e\n",
creal(result), cimag(result), error);
exact = 1.04414456540643609311;
result = cdrf(I, -I, 2.0); error = cabs(exact - result);
printf("RF(i,-i,2)=%.15f+%.15f i, 誤差=%e\n",
creal(result), cimag(result), error);
exact = 0.93912050218619371197 - 0.53296252018635269265i;
result = cdrf(I-1, I, 1.0-I); error = cabs(exact - result);
printf("RF(i-1,i,1-i)=%.15f+%.15f i, 誤差=%e\n",
creal(result), cimag(result), error);
return 0;
}
|
| コンパイル&実行 |
% gcc testcdrf.c cdrf.c % ./a.out I=0+1i count=5 RF(1,2,0)=1.311028777146060+0.000000000000000 i, 誤差=4.440892e-16 count=6 RF(i,-i,0)=1.854074677301372+0.000000000000000 i, 誤差=4.791698e-16 count=5 RF(i-1,i,0)=0.796125865842339+-1.213856669836496 i, 誤差=2.482534e-16 count=4 RF(2,3,4)=0.584082841677152+0.000000000000000 i, 誤差=0.000000e+00 count=5 RF(i,-i,2)=1.044144565406436+0.000000000000000 i, 誤差=2.279405e-16 count=5 RF(i-1,i,1-i)=0.939120502186194+-0.532962520186353 i, 誤差=2.220446e-16 |
(実は ChatGPT が「私が作りましょうか?」と言ってきたので、 任せてみたらやっぱり時間を浪費したとか (全然理解できていなくて、よくそれでそう言ってくるなあ、 とちょっと呆れた)、他にも色々な話はあるけれど、 すでに相当長くなったので、そういう枝葉は省略する。 カールソンって、子供の頃に「屋根の上のカールソン」というのがあったので、 珍しくない名前と思っていたけれど、 そういえば具体的な人の名前で出会ったのは初めてだなあ。)
(2025/6/14追記)
Carlson は 1963 年に ![]() 関数という多変数超幾何級数を導入した
(1893年の Lauricella による 3 変数超幾何級数
関数という多変数超幾何級数を導入した
(1893年の Lauricella による 3 変数超幾何級数 ![]() をもじって一般化したもの)。
それはある条件下で積分表示できて、
そのうちで楕円積分であるものが対称楕円積分ということだ。
Carlson の紹介は
https://math.nist.gov/opsf/personal/billecarlson.pdf(これは亡くなったときに、
OP-SF NET -
SIAM Activity Group on Orthogonal Polynomials and Special Functions
の電子版ニュースレター -- に載ったものらしい)
が分かりやすい。
をもじって一般化したもの)。
それはある条件下で積分表示できて、
そのうちで楕円積分であるものが対称楕円積分ということだ。
Carlson の紹介は
https://math.nist.gov/opsf/personal/billecarlson.pdf(これは亡くなったときに、
OP-SF NET -
SIAM Activity Group on Orthogonal Polynomials and Special Functions
の電子版ニュースレター -- に載ったものらしい)
が分かりやすい。
青本・喜多 [#!_______________1994!#] には、 Appell-Lauricellaの超幾何関数のことは色々書いてあるけれど、 Carlson のことは文献表に [#!Carlson1977!#] が載っているだけだ。
桂田 祐史