55 あるChatGPT 利用の記録 (プログラムを書かせたら色々やらかしてくれた)

AIの登場で、プログラミングについても、 色々な変化が起こっている (教員同士の話題にもなる)。 これまでとはやり方を変えないといけないけれど、 具体的にどうすれば良いか、走りながら考えている状態である。

ある種のことにとても役立つことは確かである。 それについても色々な情報が飛び交っている。 自分で直接確かめられたものもあるし、話として読んだだけ、というものもある。 今のところ、個人的にはかなり限定的な利用にとどまっている。

あるプログラミング言語で書いたプログラムを、 別のプログラミング言語に変換する作業は、かなりうまくやってくれる。 プログラムの翻訳と呼ぶべきだろうか。 特に翻訳後のプログラミング言語が Python の場合の作業は非常に高品質で、 とても参考になっている。

また、どのようにプログラムを書くのか、 あらかじめ自分で見通しが立てられるような場合も、 AI に指示を出して一からプログラムを書かせても (一発で解決とは行かなくても) 十分効率的に仕事が進む感じである。

一方、プログラムを作ろうとする人が、 どうすれば良いかはっきり分かっていない場合、 うまく行かないことがあるようだ。 AI に良い指示が出せないため、うまく行かない、と考えるべきだろうか。 どのようにうまく行かないのか、具体的な話を1つ紹介する。

先回りして意図を説明すると、AIは結構物知りであるが、 それを使って何か作るときに、うっかりとも言えないような、 かなりおかしなことをする場合がある。 それを読み取って AI に指摘して修正させられれば良いが、 それが出来ない場合は、 おかしなブラック・ボックスの相手を長時間することになる。

ある人が、これまでほとんど書かれたことのないプログラムを作ろうとしていた。 (新しい数値計算アルゴリズムの話で、 そのプログラムを書いた人は世界に数人しかいないだろうし、 そもそもプログラム例は1つも公開されていないであろう)。

曲面の曲率というものを計算するのが目的の1つであった。 その人は、(当然ながら) ある程度の知識があったので、 曲面の第一基本量 $E$, $F$, $G$、 第二基本量 $L$, $M$, $N$ というのを計算すれば、 それから曲率が求められるということは分かっていた。 その AI に色々質問してみると、 AIも微分幾何の基本的な知識を持っているようだった。 それでプログラムを書くように指示したのだが、それでどうなったか。

パラメーター曲面 $\bm{p}(u,v)$ に対して、 $E$, $F$, $G$ は

$$E=\bm{p}_u\cdot\bm{p}_u,\quad F=\bm{p}_u\cdot\bm{p}_v\quad G=\bm{p}_v\cdot\bm{p}_v$$

のように定義される。$\bm{p}_u$, $\bm{p}_v$ は $\bm{p}$ の偏微分係数である。 AI はこれを数値微分を使って計算するようなプログラムを書いた。

$$\bm{p}_u(u,v)\kinji \frac{\bm{p}(u+\eps,v)-\bm{p}(u,v)}{\eps},\quad \eps=10^{-5}.$$

なるほど。AI の意図したことは分からないでもない。 ただ数値微分は色々と扱いが難しいものである。 色々な注意事項が頭に浮かぶ。個人的には数値微分は避けたいものリストに入る。 それはさておき、そもそも上のような場合は、前進差分近似ではなく、

$$\bm{p}_u(u,v)\kinji \frac{\bm{p}(u+\eps,v)-\bm{p}(u-\eps,v)}{2\eps}$$

という中心差分近似を使うべきではないだろうか。 それだけで、 誤差が $O(\eps)$ から $O(\eps^2)$ に改善されるはずである。 それから実はこの問題では、普通に導関数が計算できる (出て来るのが $\log x$ なので、その微分は $\frac{1}{x}$ だというレベルの話)。

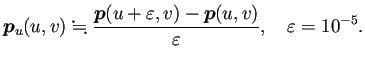
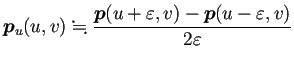
以上はちょっと気の利かないことを2つやった (数値微分の必要がないのに使った、 中心差分近似の方が良いのに前進差分近似で済ませた)、 という話だけれど、 実は AI はそれ以外にまずいこと(はっきりバグ)を2つやってくれた。

第二基本量 $L$, $M$, $N$ は、$\bm{e}$ を法線ベクトルとして

$$L=\bm{p}_{uu}\cdot\bm{e},\quad M=\bm{p}_{uv}\cdot\bm{e},\quad N=\bm{p}_{vv}\cdot\bm{e}$$

のように定義される。AI はこれも数値微分で計算しようとしたが、 その計算手順は

$$\bm{p}_{uu}(u,v)\kinji \frac{\bm{p}(u+\eps,v)-\bm{p}(u,v)}{\eps}$$

であった。あれ、これは $\bm{p}_u(u,v)$ と同じ？ 何と、2階導関数が必要なのに、1階導関数を計算している。 ちょっと信じられない間違いである。

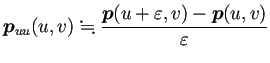
私はプログラムをざーと読んで気づいたのだけれど、 AI にプログラムを作らせた人はこのバグに気づいてなかった。 とてもおそろしい。

それからもう一つ、AI の作ったプログラムは、 $M$ と $N$ に対して同じ計算をしていた。 これも原因が分からない。 (公式の $u$ と $v$ を読み間違えて覚えていた？ そんな公式覚えたての学生の宿題の間違いみたいなことが…) まあ、上のようなひどい間違いをする位だから、 こういう間違いをしても驚くべきではないのかもしれないが。

たった1つの事例から大きなことを主張するつもりはない。 (そもそも AI は色々あるし、 1つのAIに同じ質問をしても違った答えが返って来ることも多い。 上に書いたようなバグがいつも出て来るとは考えていない。) でも、AIの出力を確認なしにそのまま受け入れることは危なくて出来ないので、 チェックが欠かせない、は言っても良いであろう。

AIの回答が参考になること自体は疑いはない。 私は数値微分を使うことは思いつかなかった。 この場合は必要がなかったけれど、 問題によってはうまい突破口になっていたかもしれない。

これからAIは改善されて、 今回の事例のような間違いはしなくなっていくことを期待している。 多分そうなるでしょう。 むしろそうなってからチェックが甘くなってしまうことの方を心配している。

連想による脱線。 30年位前、数式処理系の Mathematica を使っていて、 ときどきおかしな結果を返していて、注意しなくっちゃ、と思ったけれど、 最近はほとんど無条件で Mathematica の計算結果を信用している気がする。 まあ、証明が必要な場合は、それを書く段階で、 別の手段で確認するので大きな問題ではないような気がするけれど、 実際どうなのだろう、