18 Fresnel 積分の数値計算 (あまりMacと関係ない)

Fresnel積分

$$S(x):=\int_0^x \sin(t^2)\D t,\quad C(x):=\int_0^x \cos(t^2)\D t$$

を計算したくなった。Mathematica や Python, Julia ならば簡単である。 (MATLAB は Symbolic Math Toolbox がいるの？)

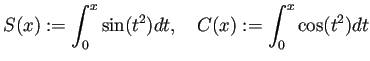
Mathematica の場合

In[ ]:=  FresnelS[1.8]
Out[ ]= 0.450939
In[ ]:=  FresnelC[1.8]
Out[ ]= 0.333633

Python の場合

>>> import scipy.special as sc
>>> sc.fresnel(1.8)
(0.45093876926758303, 0.33363292722155713)

Julia の場合

julia> using FresnelIntegrals

julia> fresnels(1.8)
0.4509387692675832 + 0.0im

julia> fresnelc(1.8)
0.3336329272215571 + 0.0im

(初めて using すると、色々たくさんインストールされてびっくりするけど。 見た通り、 結果は複素数型になるので real(fresnelc(1.8)) みたいにするものか。)

(2025/3/2追記) 2024年度の卒研でClothoid(曲線)を調べた人がいた。 それで分かったのだけれど、 これら (Mathematica, Python, Julia) で計算するのは、 正規化された Fresnel 積分というもので、 上の式で定義した $C$, $S$ を計算するには適当に直さないといけない。

ところで C や C++ だったらどうするのかな？GSLとかにあるのかな？と思ったら、 やってくれる人募集状態みたいだった。あれあれ。 もうこういうのって、Python とか Julia でやるものなのかしら。

気を取り直して検索して、https://www.netlib.org/cephes/を発見した。懐かしの NETLIB である。 ドキュメントは https://www.netlib.org/cephes/cephes.doc(拡張子が .doc になっているけれど、実はただのテキスト・ファイルなので、 .txt に直して読むのが簡単。)

もしかして Fortran コードか？と思ったけれど、C だった。 けれどもなんと、プロトタイプ宣言なしの、いわゆる第1版 K&R 流だ。 うわあ。

mkdir cephes
cd cephes
curl -O https://www.netlib.org/cephes/misc.tgz
tar xzf misc.tgz

fresnl.c と polevl.c だけで使えるのかな。 とにかく ANSI プロトタイプ宣言に直す。短いのでこれは3分で済む。 fresnl.c をコンパイルすると叱られる。 PI, PIO2, MACHEP が未定義と。 えーと、

extern double PI, PIO2, MACHEP;

なるほど、どこで定義してあるのだろう？すぐには見つからない。 でも、これって何であるか想像つくよね (PIO2 って pi over 2, MACHEP て machine epsilon だろう)。 その1行を次で置き換える。

#include <math.h>
#define PI     (M_PI)
#define PIO2   (M_PI_2)
#define MACHEP (2.2204460e-16)

(こういう書き換えは規格に適合していないかもしれないけれど。)

gcc -O3 -c fresnl.c
gcc -O3 -c polevl.c
gcc -o test_fresnl -O3 test_fresnl.c fresnl.o polevl.o

一応動いたみたい。

test_fresnl.c

#include <stdio.h>
#include <math.h>
int fresnl(double xxa, double *ssa, double *cca );

int main(void)
{
  int i,n;
  double x,dx,s,c;
  n=100;
  dx=1.0/n;
  for (i=0; i<=n; i++) {
    x=i*dx;
    fresnl(x, &s, &c);
    printf("x=%f, s=%18.15e, c=%18.15e\n", x, s, c);
  }
}

ちなみに C++ でやろうと思って「C++ の Boost には特殊関数があるんだっけ？」 と思いついたのだけれど、 Fresnel積分は入っていないのだった。 誤差関数 erf() で Fresnel 積分が計算できるかな？ と考えたのだけれど、Boost の erf() は複素数の引数を受け付けない。 まだまだですね。

どうしよう。 Arb は、任意精度だから、牛刀かしら。