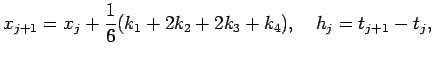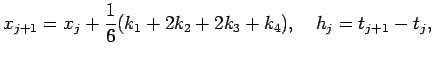

Next: A..4 RKF45 (Runge-Kutta-Fehlberg �$B8x<0�(B)
Up: A. �$B8x<0%a%b�(B
Previous: A..2 �$B8eB`�(B Euler �$BK!�(B


Next: A..4 RKF45 (Runge-Kutta-Fehlberg �$B8x<0�(B)
Up: A. �$B8x<0%a%b�(B
Previous: A..2 �$B8eB`�(B Euler �$BK!�(B
Masashi Katsurada
�$BJ?@.�(B18�$BG/�(B5�$B7n�(B3�$BF|�(B